With lots of Machine Learning algorithms out there it is often hard and confusing as to which to choose for our model especially for those who are just preparing for a big dive into data science. And no, I’m not talking about Model Selection here. Of all the algorithms there is, there has to be a simple algorithm that is well equipped and has the capability to overcome most of the complex of algorithms. KNN is one such. Both simple and in most cases elegant or at least not too disappointing.
If you are just starting your Data Science journey and you want to start humble, KNN is the best bet. Not only that it is easy to understand but you can be a master of it in a matter of minutes.
This article will get you kick-started with the KNN algorithm, understanding the intuition behind it and also learning to implement it in python for regression problems.
What is KNN And How It Works?
KNN which stands for K-Nearest Neighbours is a simple algorithm that is used for classification and regression problems in Machine Learning. KNN is also non-parametric which means the algorithm does not rely on strong assumptions instead tries to learn any functional form from the training data.
Unlike most of the algorithms with complex names, which are often confusing as to what they really mean, KNN is pretty straight forward. The algorithm considers the k nearest neighbours to predict the class or value of a data point.
Let’s try to understand it in a simple way.
Consider a hypothetical situation in which there is a new student joining your class today say Class 5. None of your friends or class teachers know him yet. Only the new student knows to which class he belongs. So he shows up during the assembly and finds his class and stands in line.
Since he is standing in the line that has only class 5 students in it, he is recognized as a Class 5 student.
KNN predicts in a very similar fashion. For example, if it was KNN predicting that which class the student belongs to, it would simply consider the closest distance between the new student and the k number of students standing next to him. The k can be any number greater than or equal to 1. If it finds out that more number of students from class 5 are closer to him than any other classes, he is recognized as a Class 5 student by KNN.
While the above example depicts a classification problem, what if we were to predict a continuous value using KNN. Well, in this case, KNN simply finds the average of all the values of the neighbouring data points and assign it to the new data point. Say for example if KNN is to predict the age of the new student in the above example, it calculates the average age of all its closest neighbours and assigns it to the new student.
The Intuitive Steps For KNN
The K Nearest Neighbour Algorithm can be performed in 4 simple steps.
Step 1: Identify the problem as either falling to classification or regression.
Step 2: Fix a value for k which can be any number greater than zero.
Step 3: Now find k data points that are closest to the unknown/uncategorized datapoint based on distance(Euclidean Distance, Manhattan Distance etc.)
Step 4: Find the solution in either of the following steps:
- If classification, assign the uncategorized datapoint to the class where the maximum number of neighbours belonged to.
or
- If regression, find the average value of all the closest neighbours and assign it as the value for the unknown data point.
Note :
For step 3, the most used distance formula is Euclidean Distance which is given as follows :
By Euclidean Distance, the distance between two points P1(x1,y1)and P2(x2,y2) can be expressed as :

Implementing KNN in Python
The popular scikit learn library provides all the tools to readily implement KNN in python, We will use the sklearn.neighbors package and its functions.
KNN for Regression
We will consider a very simple dataset with just 30 observations of Experience vs Salary. We will use KNN to predict the salary of a specific Experience based on the given data.
Let us begin!
Importing necessary libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
Loading the dataset
data = pd.read_excel("exp_vs_sal.xlsx")
You can download this simple dataset by clicking here, or you can make your own by generating a set of random numbers.
Here is what it looks like :
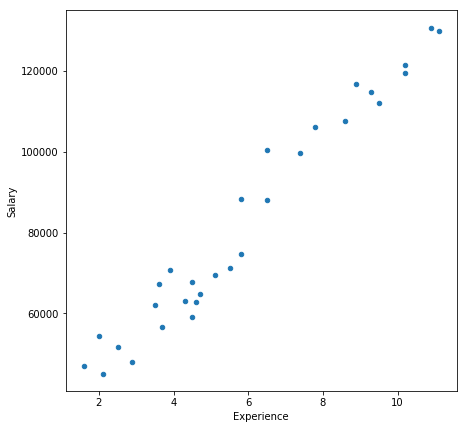
Let’s visualize the data
data.plot(figsize=(7,7))
Output:
data.plot.scatter(figsize=(7,7),x = 0, y = 1)
Output:
Creating a training set and test set
Now we will split the data set to a training set and a test set using the below code block
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(data, test_size = 0.2, random_state = 1)
Classifying the predictor(X) and target(Y)
X_train = train_set.iloc[:,0].values.reshape(-1, 1)
y_train = train_set.iloc[:,-1].values
X_test = test_set.iloc[:,0].values.reshape(-1, 1)
y_test = test_set.iloc[:,-1].values
Initializing the KNN Regressor and fitting training data
from sklearn.neighbors import KNeighborsRegressor
regressor = KNeighborsRegressor(n_neighbors = 5, metric = 'minkowski', p = 2)
regressor.fit(X_train, y_train)
Predicting Salaries for test set
Now that we have trained our KNN, we will predict the salaries for the experiences in the test set.
y_pred = regressor.predict(X_test)
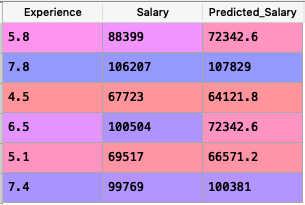
Let’s write the predicted salary back to the test_set so that we can compare.
test_set['Predicted_Salary'] = y_pred
The new test_set will look like this :
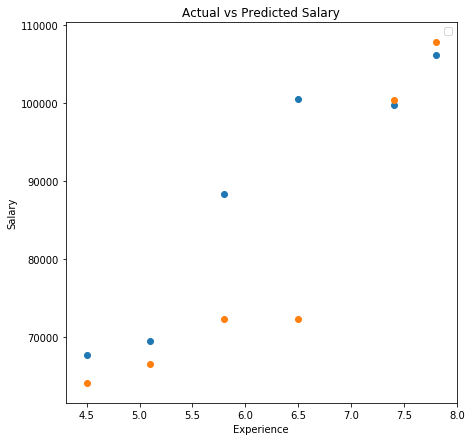
Visualizing the Predictions vs Actual Observations
plt.figure(figsize = (5,5))
plt.title('Actual vs Predicted Salary')
plt.xlabel('Age')
plt.ylabel('Salary')
plt.legend()
plt.scatter(list(test_set["Experience"]),list(test_set["Salary"]))
plt.scatter(list(test_set["Experience"]),list(test_set["Predicted_Salary"]))
plt.show()
Output
The blue points are the actual salaries as observed and the orange dots denote the predicted salaries.
From the table and the above graph, we can see that out of 6 predictions KNN predicted 4 with very close accuracy.