Reinforcement learning is one of the methods of training and validating your data under the principle of actions and rewards under the umbrella of reinforcement learning there are various algorithms and SARSA is one such algorithm of Reinforcement Learning which abbreviates for State Action Reward State Action. So in this article let us try to understand the SARSA algorithm of reinforcement learning.
Table of Contents
- The SARSA algorithm
- How is SARSA different from the Q-learning algorithm?
- How to Use SARSA Practically?
- Analyzing States and Rewards of SARSA through plots
- Summary
The SARSA algorithm
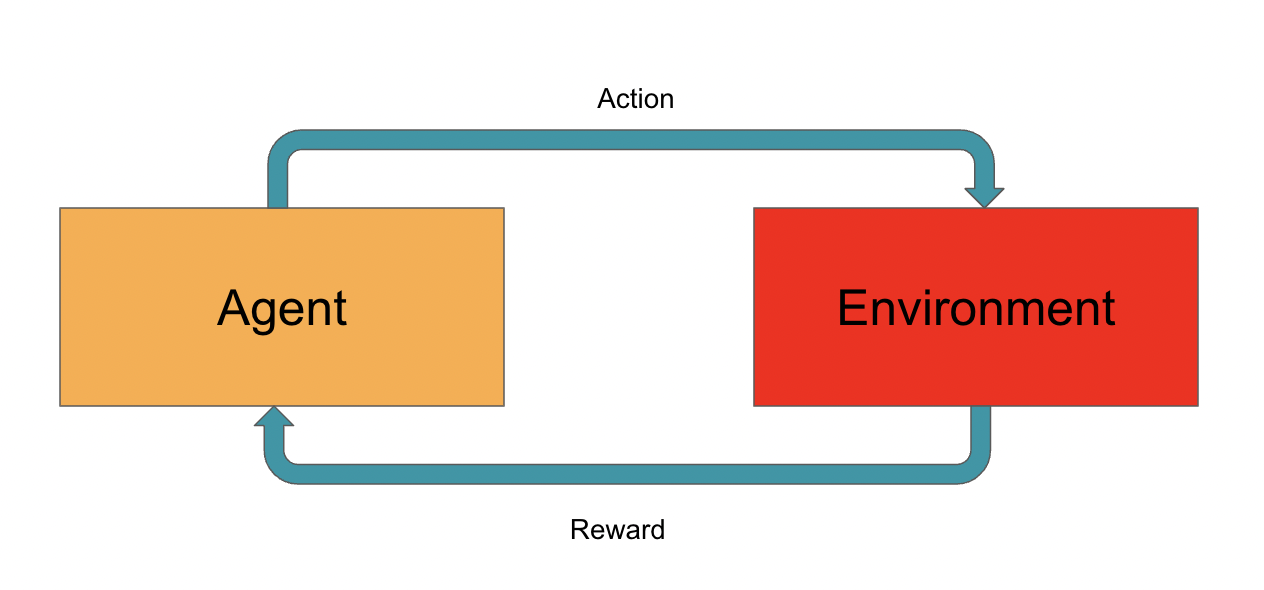
State Action Reward State Action (SARSA) is one of the algorithms of reinforcement learning which is a modified version of the Q-learning algorithm. The major point that differentiates the SARSA algorithm from the Q-learning algorithm is that it does not maximize the reward for the next stage of action to be performed and updates the Q-value for the corresponding states.
Among the two learning policies for the agent, SARSA uses the ON-policy learning technique where the agent learns from the current set of actions performed by the agents. There is no maximum operation that is being performed in the SARSA algorithm which makes it independent from the previous learning or greedy learning policy like the Q-learning algorithm.
So now let us understand how SARSA is different from the Q-learning algorithm.
How is SARSA different from the Q-learning algorithm?
| SARSA | Q-Learning |
| In the SARSA algorithm, the agent uses the On-policy for learning where the agent learns from the current set of actions in the current state and the target policy or the action to be performed. | In the Q-learning algorithm, the agent uses the off-policy learning technique where the agent learns the actions to be performed from the previous states and the awards received from the previous set of actions. |
| The learning of the agent is improved by using the current set of actions performed in the current state | The learning of the agent is improved by performing a greedy search where only the maximum reward received for the particular set of actions in that particular state is considered. |
| Previous states and previous rewards are not considered for newer states of operation | Previous states and previous rewards are considered for newer states of operations. |
How to Use SARSA Practically?
To explore SARSA practically let us design a learning policy for the agent to carry out the actions in each state and receive rewards by following the basic principle of operation of SARSA that it does not consider the maximized rewards obtained from before states and actions. So let us explore how to use SARSA practically that can be used to simulate any gaming applications or optimal solutions.
Let us create a simple SARSA environment with the help of a user-defined function with arguments as follows.
- Environment (env): Argument passed for creating an OpenAI environment
- Number of episodes: Number of iterations of agent to maximize reward
- Learning rate (alpha): Learning rate
- Discount factor: Agents choice to maximize reward
- Epsilon: random actions between 0 to 1
So before creating a user-defined function for SARSA let us create an agent using a user-defined function and declare a certain policy for learning from the different states the algorithm iterates.
Let us first install the required libraries and the official Github repository for reinforcement learning.
!git clone https://github.com/dennybritz/reinforcement-learning/
%matplotlib inline
import gym
import itertools
import matplotlib
import numpy as np
import pandas as pd
import sys
import lib
if "../" not in sys.path:
sys.path.append("../")
from collections import defaultdict
from lib.envs.windy_gridworld import WindyGridworldEnv
from lib import plotting
matplotlib.style.use('ggplot')
Now let us create an instance of the SARSA environment.
env=WindyGridworldEnv()
Now using this SARSA instance let us create a learning policy for the SARSA algorithm.
def make_epsilon_greedy_policy(Q, epsilon, nA): ## Creating a learning policy def policy_fn(observation): A = np.ones(nA, dtype=float) * epsilon / nA ## Number of actions performed best_action = np.argmax(Q[observation]) ## Maximum reward received is retrieved using argamax A[best_action] += (1.0 - epsilon) ## The best reward is subtracted from random actions return A return policy_fn
Using the learning policy let us train the SARSA algorithm on different states and actions and to collect rewards and let us use the collected reward to train the agent for the next state and actions using the user-defined function below.
def sarsa(env, num_episodes, discount_factor=1.0, alpha=0.5, epsilon=0.1):
Q = defaultdict(lambda: np.zeros(env.action_space.n)) ## Actions to be taken up by the agent
stats = plotting.EpisodeStats(episode_lengths=np.zeros(num_episodes),
episode_rewards=np.zeros(num_episodes)) ## Providing the agent states and rewards
policy = make_epsilon_greedy_policy(Q, epsilon, env.action_space.n) ## providing the agent the learning policy
## Creating various paths for the agent
for i_episode in range(num_episodes):
# Print out which episode we're on, useful for debugging.
if (i_episode + 1) % 100 == 0:
print("\rEpisode {}/{}.".format(i_episode + 1, num_episodes), end="")
sys.stdout.flush()
# Reset the environment and pick the first action
state = env.reset()
action_probs = policy(state)
action = np.random.choice(np.arange(len(action_probs)), p=action_probs)
# One step in the environment
for t in itertools.count():
next_state, reward, done, _ = env.step(action) ## Taking a step
next_action_probs = policy(next_state) ## Picking the action
next_action = np.random.choice(np.arange(len(next_action_probs)), p=next_action_probs)
stats.episode_rewards[i_episode] += reward ## Collecting the reward received by the agent for the particular state
stats.episode_lengths[i_episode] = t
td_target = reward + discount_factor * Q[next_state][next_action] ## Using discount factor to maximize reward
td_delta = td_target - Q[state][action]
Q[state][action] += alpha * td_delta
if done:
break
action = next_action
state = next_state
return Q, stats
Now as the agent is monitored for the steps and actions and also the rewards received for its action let us train the agent for the required number of iterations.
Q,stats = sarsa(env, 500)

As now the SARSA agent is iterated for the required number of iterations let us use the plotting module that is present in the official GitHub repository of reinforcement learning to validate and visualize various statistical measures of the agent like the time taken in a state to perform certain actions and the award received by the agent over different steps taken to receive the awards and other statistical measures.
Analyzing States and Rewards of SARSA through plots
So the states or the episodes taken by the agent to learn according to the learning policy used can be visualized using the plotting library of the lib module where in the agent’s time for learning through each state and the time is taken to earn the reward can be visualized.
plotting.plot_episode_stats(stats)

Let us try to interpret the above plots one by one.
The first plot is the plot that explains the time consumed by the agent to learn over different states over the period of time and the second plot shows that as gradually the agent learns for different states the time taken by the agent reduces significantly and the third plot shows that the time taken for each step increases with increase in the number of episodes for the agent.
Summary
So this is how the agent operates in the SARSA algorithm to maximize reward in each set of states and actions where the SARSA algorithm is having the ability to operate without the knowledge of previous states and actions. The SARSA algorithm entirely operates on the current learning policy and does not consider any bias in selecting only the State and Action that yielded the maximum reward to move to the next state.