Generalization and Regularization are two often terms that have the most significant role when you aim to build a robust machine learning model. The one-term refers to the model behaviour and another term is responsible for enhancing the model performance. In a straightforward way, it can be said that regularization helps the machine learning models for better generalization. In this post, we will cover each aspect of these terms and try to understand how these are linked to each other. The major points to be discussed in this article are outlined below.    

Table of Contents

1. What is Generalization?
2. Reasoning about the Generalization
3. Measuring Generalization
4. What is Regularization?
5. How Does Regularization Work?
6. Different Regularization Techniques
7. Choosing the Right Regularization Method
8. Relating Generalization and Regularization

Let’s start the discussion by understanding what generalization actually means.

What is Generalization?

The term ‘generalization’ refers to a model’s ability to adapt and react appropriately to previously unseen, fresh data chosen from the same distribution as the model’s initial input. In other words, generalization assesses a model’s ability to process new data and generate accurate predictions after being trained on a training set.

A model’s ability to generalize is critical to its success. Over-training on training data will prevent a model from generalizing. In such cases, when new data is supplied, it will make inaccurate predictions. Even if the model is capable of making accurate predictions based on the training data set, it will be rendered ineffective.

This is referred to as overfitting. The contrary is also true (underfitting), which occurs when a model is trained with insufficient data. Even given the training data, your model would fail to produce correct predictions if it was under-fitted. This would render the model as ineffective as overfitting.

Reasoning about the Generalization 

Overfitting occurs when a network performs well on the training set but performs poorly in general. If the training set contains unintentional regularities, the network may overfit. Suppose If the job is to categorize handwritten numbers, for example, it’s possible that all photos of 9s in the training set have pixel number 122 on, while all other samples have it off. 

The network may elect to take advantage of this coincidental regularity, accurately identifying all of the training samples of 9’s without having to learn the true regularities. The network will not generalize well if this property does not hold on to the test set.

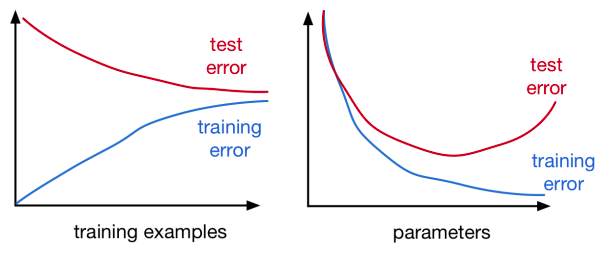
Consider how the training and generalization error fluctuates as a function of the number of training examples and the number of parameters in order to reason qualitatively about generalization. More training data should only aid generalization: the larger the training set for any given test case, the more likely there will be a closely related training example. Furthermore, as the training set grows larger, the number of accidental regularities decreases, forcing the network to focus on the real regularities.

As a result, generalization error should decrease as more training instances are added. Small training sets, on the other hand, are easier to memorize than big ones, therefore training error tends to grow as we add more examples. The two will eventually meet as the training set grows in size. This is depicted qualitatively in the figure above.

Now consider the model’s capability. The more parameters we add, the easier it is to fit both the accidental and real regularities of the training data. As a result, as we add more factors, the training error decreases. The influence on generalization mistakes is subtler. If the network has insufficient capacity, it generalizes poorly because it fails to detect regularities (whether true or accidental) in the data. It will memorize the training set and fail to generalize if it has too much capacity.

As a result, capacity has a non-monotonic influence on test error: it decreases and then increases. We’d like to create network topologies that are powerful enough to learn actual regularities in training data but not powerful enough to merely remember the training set or exploit accidental regularities. This is depicted qualitatively in the figure above.

Measuring Generalization

In most scenarios, we generally focused on the training set or tried to optimize the performance on the training set. But this is not the correct way of model building, there is a lot of uncertainty (such as noise) in the unseen data which is taken from the same distribution as the training set. So in such cases, we also should aim for our model that can generalize well on those unseen data.   

Fortunately, there is a simple method for assessing a model’s generalization performance. Simply put, we divide our data into three subsets.

• A training set is a collection of training examples on which the network is trained.
• A validation set is used to fine-tune hyperparameters like the number of hidden units and the learning rate.
• A test set designed to evaluate generalization performance.

The losses on these subsets are referred to as training, validation, and test loss, in that order. It should be evident why we need distinct training and test sets: if we train on test data, we have no notion if the model is correctly generalizing or merely memorizing the training examples. 

There are other variations on this basic method, including what is known as cross-validation. These options are typically employed in cases with tiny datasets, i.e. less than a few thousand examples. The majority of advanced machine learning applications include datasets large enough to be divided into training, validation, and test sets.

Apart from all these techniques, there is one called Regularization. Regularization has no effect on the algorithm’s performance on the data set used to learn the model parameters (feature weights). It can, however, increase generalization performance, i.e., performance on new, previously unknown data, which is exactly what we want. 

What is Regularization?

In general, the term “regularization” refers to the process of making something regular or acceptable. This is precisely why we utilize it for machine learning applications. Regularization is the process of shrinking or regularizing the coefficients towards zero in machine learning. To put it another way, regularization prevents overfitting by discouraging the learning of a more complicated or flexible model.

While modelling in regression analysis, the features are calculated using coefficients. Furthermore, if the estimates can be constrained, shrunk, or regularized towards zero, the impact of trivial features can be decreased, and models with high variance and a stable fit can be avoided.

How does Regularization Work?

The main concept is to penalize complex models by including a complexity factor that causes a larger loss for complex models. Consider a basic linear regression relationship to better comprehend it. It is stated mathematically as follows:

Y≈ W₀+ W₁ X₁+ W₂ X₂+⋯+W_P X_P

Where Y denotes the learned relationship or the expected value. X₁, X₂,…, X_P are the characteristics that determine the value of Y. The weights allocated to the attributes X₁, X₂,…, X_P are W₁, W₂,…, W_P. W₀ is used to symbolize bias.

To build a model that reliably predicts the value of Y, we’ll need a loss function and ideal parameters like bias and weights. In linear regression, the residual sum of the squares loss function is often used.

The model will now learn using this loss function. It will alter the weights based on our training data (coefficients). If our dataset is noisy, it will suffer from overfitting, and the calculated coefficients will not generalize to previously unknown data.

Here is where regularization comes into play. It penalizes the magnitude of coefficients to regularize these learned estimations towards zero. But first, let’s look at how it imposes a penalty to the coefficients.

Different Regularization Techniques

Each of the strategies below uses a different regularization norm (L-p) depending on the mathematical methodology that generates several types of regularization. The beta coefficients of the characteristics are affected differently by these techniques. The following are some machine learning regularization techniques:

Most of the methods below use L1 and L2 norms. The L1 norm is calculated by adding the absolute values of the vector. The L2 norm is calculated by taking the square root of the sum of the squared vector values.

Lasso Regression

The coefficients are penalized to the point where they reach zero in the Least Absolute Shrinkage and Selection Operator (or LASSO) Regression. It gets rid of the unimportant independent variables. The L1 norm is used for regularization in this technique.

• L1-norm is added as a penalty.
• The beta coefficients’ absolute value is L1.
• The L1 regularization is another name for it.
• L1 regularization produces sparse results.

When there are a lot of variables, this strategy comes in handy because it may be utilized as a feature selection method on its own.

Ridge Regression 

When the variables in a model are multicollinear, the Ridge regression approach is employed to analyze it. It minimizes the number of inconsequential independent variables but does not totally eliminate them. The L2 norm is used for regularization in this sort of regularization. As a punishment, it employs the L2-norm.

• The L2 penalty is equal to the square of the magnitudes of the beta coefficients.
• It is also referred to as L2-regularization.
• L2 reduces the coefficients but never brings them to zero.
• L2 regularization produces non-sparse results.

Choosing the Right Regularization Method

Ridge regression is employed when all of the independent variables in the model must be included, or when there are multiple interactions. There is collinearity or codependency between the variables in this case.

When there are multiple predictors available and we want the model to do feature selection for us, we use Lasso regression.

When there are a lot of variables and we can’t decide whether to use Ridge or Lasso regression, Elastic-Net regression is the best option.

Relating Generalization and Regularization

By the discussion so far we can summarize generalization and regularization as below so that we can find a relationship between both the concepts.

• The term generalization is used to describe how the model is good at predicting the new instances which it didn’t see before. Ideally speaking the model should generalize the relationship as same as during the training phase. Whereas the term regularization is referred to as a process that enhances the generalization capabilities of the model.
• The poor generalization is due to problems like overfitting, underfitting, and bias-variance issues. We can easily interpret the generalization status of our model by just observing the training and validation accuracy or testing accuracy scores. 
• Whenever there is a poor generalization we apply one of the regularization techniques mentioned above based on the method It penalizes the magnitude of coefficients which is responsible for generalization towards zero. 

Conclusion 

Through this post, we have seen two important terminologies that every professional and novice should know. To summarize, the generalization is a process, or, can be called a remark of your ML model that tells us how the model is good at predicting or estimating the true relationship of unseen data points. Whereas regularization, the name itself tells us that it regularizes the behaviour of your ML model, or in other terms, it enhances the generalization process.  

References 

• Generalization
• What Is Regularisation?