A Hidden Markov Model (HMM) is a statistical model which is also used in machine learning. It can be used to describe the evolution of observable events that depend on internal factors, which are not directly observable. These are a class of probabilistic graphical models that allow us to predict a sequence of unknown variables from a set of observed variables. In this article, we will discuss the Hidden Markov Models in detail. We will understand the contexts where it can be used and we will also discuss its different applications. We will also discuss the use of HMM for PoS tagging with python implementation. The major points to be covered in the article are listed below.
Table of Contents
- Hidden Markov Model
- Hidden Markov Model With an Example
- Application of Hidden Markov Model
- Hidden Markov Models in NLP
- What is PoS-tagging?
- PoS Tagging with Hidden Markov Model
- Implementation in Python
Hidden Markov Model
The Hidden Markov model is a probabilistic model which is used to explain or derive the probabilistic characteristic of any random process. It basically says that an observed event will not be corresponding to its step-by-step status but related to a set of probability distributions. Let’s assume a system that is being modelled is assumed to be a Markov chain and in the process, there are some hidden states. In that case, we can say that hidden states are a process that depends on the main Markov process/chain.
The main goal of HMM is to learn about a Markov chain by observing its hidden states. Considering a Markov process X with hidden states Y here the HMM solidifies that for each time stamp the probability distribution of Y must not depend on the history of X according to that time.
Hidden Markov Model With an Example
To explain it more we can take the example of two friends, Rahul and Ashok. Now Rahul completes his daily life works according to the weather conditions. Major three activities completed by Rahul are- go jogging, go to the office, and cleaning his residence. What Rahul is doing today depends on whether and whatever Rahul does he tells Ashok and Ashok has no proper information about the weather But Ashok can assume the weather condition according to Rahul work.
Ashok believes that the weather operates as a discrete Markov chain, wherein the chain there are only two states whether the weather is Rainy or it is sunny. The condition of the weather cannot be observed by Ashok, here the conditions of the weather are hidden from Ashok. On each day, there is a certain chance that Bob will perform one activity from the set of the following activities {“jog”, “work”,” clean”}, which are depending on the weather. Since Rahul tells Ashok that what he has done, those are the observations. The entire system is that of a hidden Markov model (HMM).
Here we can say that the parameter of HMM is known to Ashok because he has general information about the weather and he also knows what Rahul likes to do on average.
So let’s consider a day where Rahul called Ashok and told him that he has cleaned his residence. In that scenario, Ashok will have a belief that there are more chances of a rainy day and we can say that belief Ashok has is the start probability of HMM let’s say which is like the following.
The states and observation are:
states = ('Rainy', 'Sunny')
observations = ('walk', 'shop', 'clean')
And the start probability is:
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
Now the distribution of the probability has the weightage more on the rainy day stateside so we can say there will be more chances for a day to being rainy again and the probabilities for next day weather states are as following
transition_probability = {
'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
}From the above we can say the changes in the probability for a day is transition probabilities and according to the transition probability the emitted results for the probability of work that Rahul will perform is
emission_probability = {
'Rainy' : {'jog': 0.1, 'work': 0.4, 'clean': 0.5},
'Sunny' : {'jog': 0.6, 'work: 0.3, 'clean': 0.1},
}This probability can be considered as the emission probability. Using the emission probability Ashok can predict the states of the weather or using the transition probabilities Ashok can predict the work which Rahul is going to perform the next day.
Below image shown the HMM process for making probabilities

So here from the above intuition and the example we can understand how we can use this probabilistic model to make a prediction. Now let’s just discuss the applications where it can be used.
Application of Hidden Markov Model
An application, where HMM is used, aims to recover the data sequence where the next sequence of the data can not be observed immediately but the next data depends on the old sequences. Taking the above intuition into account the HMM can be used in the following applications:
- Computational finance
- speed analysis
- Speech recognition
- Speech synthesis
- Part-of-speech tagging
- Document separation in scanning solutions
- Machine translation
- Handwriting recognition
- Time series analysis
- Activity recognition
- Sequence classification
- Transportation forecasting
Hidden Markov Models in NLP
From the above application of HMM, we can understand that the applications where the HMM can be used have sequential data like time series data, audio, and video data, and text data or NLP data. In this article, our main focus is on those applications of NLP where we can use the HMM for better performance of the model, and here in the above-given list, we can see that one of the applications of the HMM is that we can use it in the Part-of-Speech tagging. Next in the article, we will see how we can use the HMM for POS-tagging.
What is POS-tagging?.
We have learned in our school timings that the part of speech indicates the function of any word, like what it means in any sentence. There are commonly nine parts of speeches; noun, pronoun, verb, adverb, article, adjective, preposition, conjunction, interjection, and a word need to be fit into the proper part of speech to make sense in the sentence.
POS tagging is a very useful part of text preprocessing in NLP as we know that NLP is a task where we make a machine able to communicate with a human or with a different machine. So it becomes compulsory for a machine to understand the part of speech.
Classifying words in their part of speech and providing their labels according to their part of speech is called part of speech tagging or POS tagging OR POST. Hence the set of labels/tags is called a tagset. In the article, we have seen how we can implement the part of speech at a beginning level using the NLTK where the tagsets package of NLTK was helping us to provide the part of speech tag to our documents.
POS Tagging With Hidden Markov Model
We can say that in the case of HMM is a stochastic technique for POS tagging. Let’s take an example to make it more clear how HMM helps in selecting an accurate POS tag for a sentence.
As we have seen in the example of the HMM process in POS tagging the transition probability is the likelihood of any sequence for example what are the chances for a noun word to come after any modal and a modal after a verb and a verb after a noun.
Let’s take the sentence “Rahul will eat food” where Rahul is a noun, will is a modal, eat is a verb and food is also a noun, so the probability for a word to be in a particular class of part of speech is called the Emission probability.
Let’s take a look at how we can calculate these two probabilities for a set of sentences:
- Mary Jane can see will
- The spot will see Mary
- Will Jane spot Mary?
- Mary will pat Spot
The below table is a counting tableau for the words with their part of speech type
| Words | Noun | Modal | Verb |
| mary | 4 | 0 | 0 |
| jane | 2 | 0 | 0 |
| will | 1 | 3 | 0 |
| spot | 2 | 0 | 1 |
| can | 0 | 1 | 0 |
| see | 0 | 0 | 2 |
| pat | 0 | 0 | 1 |
Let’s divide each word’s appearance by the total number of every part of speech in the set of sentences.
| Words | Noun | Modal | Verb |
| mary | 4/9 | 0 | 0 |
| jane | 2/9 | 0 | 0 |
| will | 1/9 | 3/4 | 0 |
| spot | 2/9 | 0 | 1/4 |
| can | 0 | 1/4 | 0 |
| see | 0 | 0 | 2/4 |
| pat | 0 | 0 | 1/4 |
Here in the table, we can see the emission probabilities of every word.
Now as we have discussed that the transition probability is the probability of the sequences we can define a table for the above set of sentences according to the sequence of part of speech.
| Noun | Modal | Verb | End | |
| Start | 3 | 1 | 0 | 0 |
| Noun | 1 | 3 | 1 | 4 |
| Model | 1 | 0 | 3 | 0 |
| Verb | 4 | 0 | 0 | 0 |
Now in the table, we are required to check for the combination of parts of speeches for calculation of the transition probabilities. For example, we can see in the set of sentences modal before a verb has appeared 3 times and 1 time before a noun. This means it has appeared in the set for four-time and the probability of coming modal before any verb will be ¾ and before a noun will be ¼. Similarly performing this for every entity of the table:
| Noun | Modal | Verb | End | |
| Start | 3/4 | 1/4 | 0 | 0 |
| Noun | 1/9 | 3/9 | 1/9 | 4/9 |
| Model | 1/4 | 0 | 3/4 | 0 |
| Verb | 4/4 | 0 | 0 | 0 |
Here the above values in the table are the respective transition values for a given set of sentences.
Let’s take the sentence “Will Jane spot Mary?” out from the set and now we can calculate the probabilities for every part of speech using the above calculations.
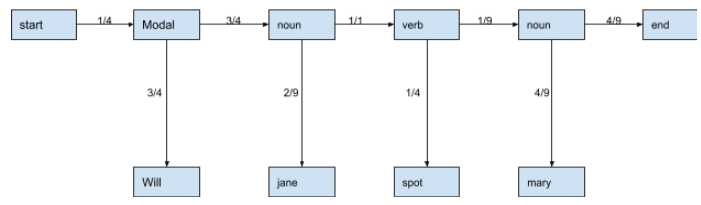
In the above image, we can see that we have emission probabilities of the words in the sentence given in the vertical lines and the horizontal lines are representing all the transition probabilities.
Now the correctness of the POS tagging is measured by the product of all these probabilities. The product of probabilities represents the likelihood that the sequence is right.
Let’s just check for the rightness of the POS tagging.
¼*¾*¾*2/9*1/1*¼*1/9*4/9*4/9 = 0.0001714678
Here we can see that the product is higher than zero which means the POS tagging we have performed is correct and if the result is zero then the tagging performed will not be correct.
So here we have seen how the HMM,s algorithm works for providing the POS tagging to the sentences but the example was small where we had only 3 kinds of POS tags but there are 81 different kinds of POS tags available. When it comes to finding the number of combinations from a small data set it can be done with smaller efforts but when it comes to tagging larger sentences and finding the right sequences with all the 81 tags the number of combinations increases exponentially. The computation may cause a larger effect but the more number of POS tags gives more accuracy.
To optimize the implementation of HMM for POS tagging we can use the Viterbi algorithm which is a dynamic programming algorithm. Using this algorithm we can obtain the maximum posterior probability estimate of the most likely sequence of hidden states. Especially in the context of HMM. for more details about the algorithm you can check it on this link.
Implementation in Python
By taking care of the size of the article I am posting only results and steps which I have followed to implement and optimize the HMM using the Viterbi Algorithm. The reader can access this link for the codes.
For implementation, I have used the NLTK provided Treebank dataset and applied the tags on them using the universal_tagset package of NLTK.
The below image is a representation of the words with the tags on them presented in the dataset.

In the data which we are using we have 12 unique tags on it. Like the following image.

The below image represents the transition probability table.

In the table we can see that we have almost no zero values. By this also we can say the tagging on the data is almost correct also we can optimize it using the Viterbi algorithm.

The above-given image is a result of ten sentences of the data set where we can see that we almost get 94% accuracy. which is good enough which means after this we can proceed with the next step of our project. Since the dataset I am using can be considered as the ideal data which is already processed. In any real-life cases to obtain more accuracy, we can use some more modifications on the data like providing more rules so that the tagging procedure can be done more accurately by implementing more tags on the data.
Final words
In the article, we have seen the definition and the explanation of the hidden Markov model. There can be various applications of this model. As the intuition of the hidden Markov model we can say that it mainly has applications in the fields where the data is sequential and taking it into consideration we have seen that how it can be beneficial for us in part of speech tagging which plays a crucial role in any NLP project and how easily we can perform it accurately.
Popular Guides