Dropout is an important regularization technique used with neural networks. Despite effective results in general neural network architectures, this regularization has some limitations with the convolutional neural networks. Due to this reason, it does not solve the purpose of building robust deep learning models. DropBlock is a regularization technique, which was proposed by the researchers at Google Brain, addresses the limitations of the general dropout scheme and helps in building effective deep learning models. This article will cover the DropBlock regularization methodology, which outperforms existing regularization methods significantly. Following are the topics to be covered.

Table of contents

1. About the dropout method of regularization
2. Reason to introduce DropBlock
3. About DropBlock
4. How to set the hyperparameters
5. Syntax to use DropBlock

By preserving the same amount of features, the regularization procedure minimizes the magnitude of the features. Let’s start with the Dropout method of regularization to understand DropBlock.

About the dropout method of regularization

Deep neural networks include several non-linear hidden layers, making them highly expressive models capable of learning extremely complex correlations between their inputs and outputs. However, with minimal training data, many of these complex associations will be the consequence of sampling noise, thus they will exist in the training set but not in the true test data, even if they are derived from the same distribution. This leads to overfitting, and several ways for decreasing it have been devised. These include halting training as soon as performance on a validation set begins to deteriorate.

There are two best ways to regularize a fixed-sized model.

• By calculating a geometric mean of the predictions of an exponential number of learnt models with shared parameters.
• By combining different models, it could be expensive to take an average of the outputs and hard to train models with different architectures.

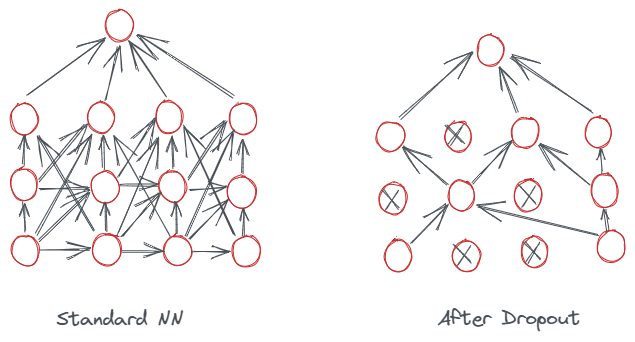
Dropout is a regularization strategy that solves two difficulties. It eliminates overfitting and allows for the efficient approximation combination of exponentially many distinct neural network topologies. The word “dropout” refers to the removal of units (both hidden and visible) from a neural network. Dropping a unit out means removing it from the network momentarily, including with all of its incoming and outgoing connections. The units to be dropped are chosen at random.

A thinned network is sampled from a neural network by applying dropout. All the units that avoided dropout make up the thinning network. A collection of potential “2 to the power of nets” thinning neural networks may be considered a neural network with a certain number of units. Each of these networks shares weights in order to keep the total number of parameters at the previous level or lower. A new thinning network is sampled and trained each time a training instance is presented. Therefore, training a neural network with dropout may be compared to training a group of “2 to the power of nets” thinned networks with large weight sharing, where each thinned network is trained extremely infrequently or never.

Are you looking for a complete repository of Python libraries used in data science, check out here.

Reason to introduce DropBlock

A method for enhancing neural networks is a dropout, which lowers overfitting. Standard backpropagation learning creates brittle co-adaptations that are effective for the training data but ineffective for data that has not yet been observed. These co-adaptations are disrupted by random dropout because it taints the reliability of any one concealed unit’s existence. However, removing random characteristics is a dangerous task since it might remove anything crucial to solving the problem.

To deal with this problem DropBlock method was introduced to combat the major drawback of Dropout being dropping features randomly which proves to be an effective strategy for fully connected networks but less fruitful when it comes to convolutional layers wherein features are spatially correlated.

About DropBlock

In a structured dropout method called DropBlock, units in a feature map’s contiguous area are dropped collectively. Because activation units in convolutional layers are spatially linked, DropBlock performs better than dropout in convolutional layers. Block size and rate (γ) are the two primary parameters for DropBlock.

• Block size refers to the block’s size before it is discarded.
• Rate (γ) determines the number of activation units dropped.

Similar to dropout, the DropBlock is not applied during inference. This may be understood as assessing an averaged forecast over the ensemble of exponentially growing sub-networks. These sub-networks consist of a unique subset of sub-networks covered by dropout in which each network does not observe continuous feature map regions.

How to set the hyperparameters

There are two main hyperparameters on which the whole algorithm works which are block size and the rate of unit drop.

Block size

The feature map will have more features to drop as every zero entry on the sample mask is increased to block size, the block size is sized 0 blocks, and so will the percentage of weights to be learned during training iteration, thus lowering overfitting. Because more semantic information is removed when a model is trained with bigger block size, the regularization is stronger.

According to the researchers, regardless of the feature map’s resolution, the block size is fixed for all feature maps. When block size is 1, DropBlock resembles Dropout, and when block size encompasses the whole feature map, it resembles SpatialDropout.

Rate of drop 

The amount of characteristics that will be dropped depends on the rate parameter (γ). In dropout, the binary mask will be sampled using the Bernoulli distribution with a mean of “1-keep_prob,” assuming that we wish to keep every activation unit with the probability of “keep_prob”.

• The chance of keeping a unit is known as keep_prob. This regulates the level of dropout. Since probability is 1, there should be no dropouts, and low probability values indicate more dropouts. 

We must, however, alter the rate parameter (γ) when we sample the initial binary mask to take into account the fact that every zero entry in the mask will be extended by block size2 and the blocks will be entirely included in the feature map. DropBlock’s key subtlety is that some dropped blocks will overlap, hence the mathematical equation can only be approximated.

The effect of hyperparameters

Let’s understand with an example shown in the below image, it represents the test results by researchers. The researchers applied DropBlock on the ResNet-50 model to check the effect of block size. The models are trained and evaluated with DropBlock in groups 3 and 4. So two ResNet-50 models were trained.

1. Model with block_size = 7 and keep_prob = 0.9 
2. Model with block_size = 1 and keep_prob = 0.9.

The first model has higher accuracy compared to the second ResNet-50 model.

Syntax to use DropBlock

The syntax provided by Keras to use DropBlock for regularizing the neural networks is shown below.

keras_cv.layers.DropBlock2D(rate, block_size, seed=None, **kwargs)

Hyperparameter: 

• rate: Probability of dropping a unit. Must be between 0 and 1.
• block_size: The size of the block to be dropped. It could be defined in a single integer value or tuple of integers.

Conclusion

DropBlock’s resilience is demonstrated by the fact that it drops semantic information more effectively than the dropout. Convolutional layers and fully connected layers might both use it. With this article, we have understood about DropBlock and its robustness.

References

• Research paper on DropBlock
• Documentation by Keras