The Principal Component Analysis is a popular unsupervised learning algorithm that is widely known for dimensionality reduction. It increases the interpretability and also reduces the loss of information while reducing the dimensionality. It helps to find the most significant feature in a dataset and makes the data easy for plotting in 2D and 3D and it also helps in finding the sequence of linear combinations of variables.
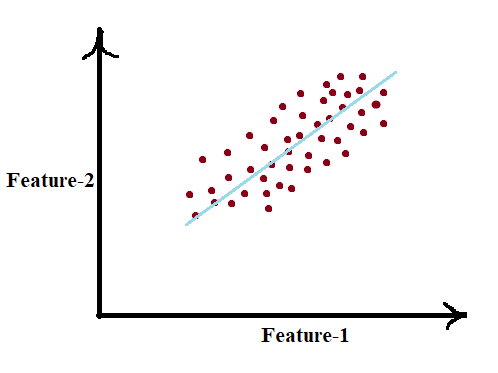
In the above figure we have several points plotted on a 2D plot, plotted based on the information of Feature-1 and 2. Here the key point of PCA is dimensionality reduction which is the process of reducing the number of dimensions (Features/Attributes) of the given dataset. From the above figure, it is clearly visible that all the points are directed and it seems to have a linear trend, thus applying PCA on such data we can easily reduce the 2D data into 1D.
Moreover, we could also see that all the points vary most along the blue line more than either axis. This means if we know the position of a point and that lies on the blue line then we have more information of that point rather than knowing location along with either of Feature-1 or 2. Hence PCA can really help us to find the direction along which our data varies the most.
By running PCA on a set of data points we come up with the two principal components which are also referred to as eigenvectors. Those are straight lines that capture most of the variance of data and it comprises the information of direction and magnitude of data points.
From the below graph we can see that there are two Principal components, the green one primary component which explains the maximum variance and the blue one is orthogonal to the green vector.

The size of the above eigenvectors is encoded in the eigenvalues, the beginning of these vectors is the centre point for all the points. For more mathematical intuition refer to this wiki link.
Today in this article we are going to see the practical use case of PCA. Here we leverage the effectiveness of PCA to detect the orientation of different objects in a particular image. After running the PCA we will come with the result as shown in the above figure.
Determination of the orientation of objects
As we are dealing with images we need to work with OpenCV as it is more flexible when it comes to image handling and manipulation and also we use PCA from the cv2.PCAComponent2 class.
Import all dependencies:
import numpy as np
# to compute angles
from math import atan2, cos, sin, sqrt, pi
from google.colab.patches import cv2_imshow
import cv2Read and preprocess the image:
Here we load the image and apply necessary transformations so that we can detect objects
# load image
src = cv2.imread('/content/sample.png')
cv2_imshow(src)
# convert to grayscale
gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
# convert img into binary
_, bw = cv2.threshold(gray, 50, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU)
# calculating Contours
contours, _ = cv2.findContours(bw, cv2.RETR_LIST, cv2.CHAIN_APPROX_NONE)Necessary functions:
get_orientation() function is used to perform PCA which extract the orientation of interested objects and draw_axis() is used to draw contours and components.
def get_orientation(pts, img):
sz = len(pts)
data_pts = np.empty((sz, 2), dtype=np.float64)
for i in range(data_pts.shape[0]):
data_pts[i,0] = pts[i,0,0]
data_pts[i,1] = pts[i,0,1]
# Perform PCA analysis
mean = np.empty((0))
mean, eigenvectors, eigenvalues = cv2.PCACompute2(data_pts, mean)
# Store the center of the object
cntr = (int(mean[0,0]), int(mean[0,1]))
cv2.circle(img, cntr, 3, (255, 0, 255), 2)
p1 = (cntr[0] + 0.02 * eigenvectors[0,0] * eigenvalues[0,0], cntr[1] + 0.02 * eigenvectors[0,1] * eigenvalues[0,0])
p2 = (cntr[0] - 0.02 * eigenvectors[1,0] * eigenvalues[1,0], cntr[1] - 0.02 * eigenvectors[1,1] * eigenvalues[1,0])
draw_axis(img, cntr, p1, (0, 150, 0), 1)
draw_axis(img, cntr, p2, (200, 150, 0), 5)
angle = atan2(eigenvectors[0,1], eigenvectors[0,0]) # orientation in radians
return angledef draw_axis(img, p_, q_, colour, scale):
p = list(p_)
q = list(q_)
angle = atan2(p[1] - q[1], p[0] - q[0]) # angle in radians
hypotenuse = sqrt((p[1] - q[1]) * (p[1] - q[1]) + (p[0] - q[0]) * (p[0] - q[0]))
# Here we lengthen the arrow by a factor of scale
q[0] = p[0] - scale * hypotenuse * cos(angle)
q[1] = p[1] - scale * hypotenuse * sin(angle)
cv2.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv2.LINE_AA)
# create the arrow hooks
p[0] = q[0] + 9 * cos(angle + pi / 4)
p[1] = q[1] + 9 * sin(angle + pi / 4)
cv2.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv2.LINE_AA)
p[0] = q[0] + 9 * cos(angle - pi / 4)
p[1] = q[1] + 9 * sin(angle - pi / 4)
cv2.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv2.LINE_AA)Extract objects based on the area of interest:
Here we find the relevant contours based by filtering the size of it
for i,c in enumerate(contours):
# area of each contour
area = cv2.contourArea(c)
# ignore contour which is too small or large
if area < 1e2 or 1e5 < area:
continue
# draw each contour only for visualization
cv2.drawContours(src, contours, i, (0, 0, 255), 2)
# find orientation of each shape
get_orientation(c,src)Here below we can obtain the result of our orientation;
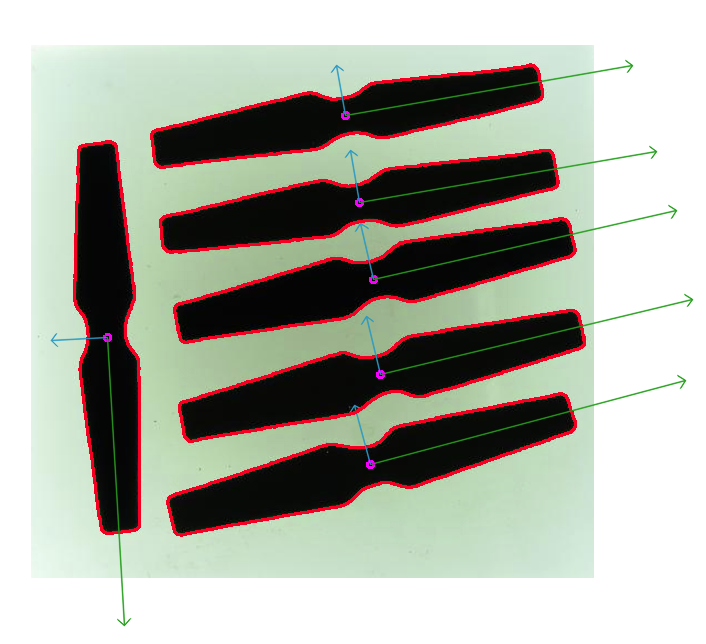
As you can see the results are so precise and accurate.
Conclusion:
In this article, we have seen how to detect the orientation of given objects using PCA and OpenCV. As you can see the first principal component is directed so well which gives the clear orientation of objects. Further one can explore this code to detect the orientation of different kinds of objects and see the interesting result.



















































































