In machine learning, deterministic and stochastic methods are utilised in different sectors based on their usefulness. A deterministic process believes that known average rates with no random deviations are applied to huge populations. A stochastic process, on the other hand, defines a collection of time-ordered random variables that reflect the potential sample pathways. In this article, we will be discussing the key differences between their functioning and their applications. The major points to be discussed in this article are outlined below.
Table of contents
- Deterministic and Stochastic process modelling
- When could they both be used?
- How do these approaches work?
- Different forms of stochastic and deterministic algorithms
- Benefits and drawbacks of Deterministic and Stochastic
- Applications of Deterministic and Stochastic algorithms
Let’s start with a high-level overview of deterministic and stochastic processes.
Deterministic and Stochastic process modelling
Deterministic modelling produces consistent outcomes for a given set of inputs, regardless of how many times the model is recalculated. The mathematical characteristics are known in this case. None of them is random, and each problem has just one set of specified values as well as one answer or solution. The unknown components in a deterministic model are external to the model. It deals with the definitive outcomes as opposed to random results and doesn’t make allowances for error.
In contrast, stochastic modelling is intrinsically unpredictable, and the unknown components are integrated into the model. The model generates a large number of answers, estimates, and outcomes, much like adding variables to a difficult maths problem to see how they affect the solution. The identical procedure is then done several times in different settings.

Are you looking for a complete repository of Python libraries used in data science, check out here.
When could they both be used?
A deterministic model is applied where outcomes are precisely determined through a known relationship between states and events where there is no randomness or uncertainty.
For example, If we know that consuming a fixed amount of sugar ‘y’ will increase the fat in one’s body by ‘2x’ times. Then ‘y’ can always be determined exactly when the value of ‘x’ is known.
Similarly, when the relationship between variables is unknown or uncertain then stochastic modelling could be used because it relies on likelihood estimation of the probability of events.
For example, the insurance sector primarily depends on stochastic modelling to forecast how firm balance sheets will appear in the future.
How do these approaches work?
As deterministic models show the relationship between results and the factors affecting the outcomes. For this kind of model, the relationship between the variables should be known or determined.
Let’s consider building a machine learner that can help an athlete in a 100-metre sprint, the most important factor in the 100-metre sprint is time. The objective of the model would be to minimize the time of the athlete. The two most important factors affecting time are speed and distance.
The distance covered by every athlete is the same, it’s constant for everyone, the only thing that varies is speed. But varying speed could be controlled as the factors affecting speed are known as the position of the body, the flight time, etc. Since we know time is dependent on speed and distance this makes this problem deterministic.

The stochastic aspect of machine learning algorithms is most evident in complicated and nonlinear approaches used to solve classification and regression predictive modelling issues. These methods employ randomization in the process of building a model from the training data, resulting in a different model fitting each time the same algorithm is performed on the same data.
As a result, when tested on a holdout test dataset, the slightly modified models perform differently. Because of this stochastic behaviour, the model’s performance must be described using summary statistics that indicate the model’s mean or predicted performance rather than the model’s performance from any single training session.
Let’s consider a die-rolling problem. You are rolling a die in a casino. If you roll a six or a one, you win the cash prize. Initially, a sample space that includes all possibilities for die roll outcomes will be generated. The probability for any number being rolled is computed which is ‘0.17’. But we are only interested in two numbers, ‘6’ and ‘1’. So the final probability would be 0.33. This is how a stochastic model would work.
Let’s have a look at how a linear regression model can work both as a deterministic as well as a stochastic model in different scenarios.
Deterministic models define a precise link between variables. In the deterministic scenario, linear regression has three components. The dependent variable ‘y’, the independent variable ‘x’ and the intercept ‘c’. There is no room for mistakes in predicting y for a given x. Here is an equation as an example to replicate the above explanation.
F=95C+32
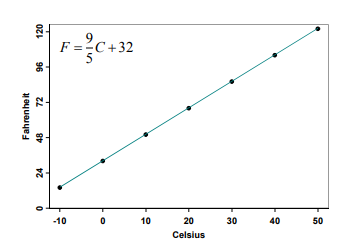
The above equation would have a graph something like this with all data points in a straight line.
A stochastic model that takes into account random error. There is a deterministic component as well as a random error component. A probabilistic link between y and x is hypothesised in this paradigm. Here is an equation as an example to replicate the above explanation.
y= 1.5x+error

In the above graph, it could be observed that due to the error component in the linear regression equation there is randomness in the data.
Different forms of stochastic and deterministic algorithms
Principal Component Analysis (PCA)
PCA is a deterministic approach as there are no parameters to initialize. PCA finds the line through the centroid with the smallest sum of squared distances between the points given a set of points in n-dimensional space. Identifying the line for which the projections of the points onto that line are as large as feasible is the same thing (as measured by the sum of squared lengths).
Then, subject to the restriction of being orthogonal to the first line, it finds the line through the centroid with the smallest sum of squared distances to the points. The third principle component, the fourth, and so on. Because all of these procedures are simply geometric, the main components are deterministic data functions.
Weighted nearest neighbours
A weighted nearest neighbours method also could be called a basic KNN is a deterministic method. This technique employs a statistic known as the “Weighing function.” The weight is determined by taking the inverse of the distance. Because the distance between each data point and the query point would be the same in each iteration, the weights would be a deterministic term.
Poissons Process
The Poisson method is a stochastic process that displays a random number of points or occurrences across time. The number of points in a process that falls between zero and a specific period is characterised as a time-dependent Poisson random variable. The index set of this process is made up of non-negative integers, whereas the state space is made up of natural numbers. This approach is known as the Poisson counting process because it may be thought of as a counting operation.
Bernoulli Process
The Bernoulli process is a set of randomly distributed random variables, each with a chance of one or zero. This procedure is analogous to continually flipping a coin, with the probability of winning being p and the value being one, and the likelihood of obtaining a tail being zero. As the result is probabilistic that’s the reason this method is a stochastic process.
Random Walk
The simple random walk is a discrete-time stochastic process using integers as the state space that is based on a Bernoulli process with each Bernoulli variable taking either a positive or a negative value.
Benefits and drawbacks of Deterministic and Stochastic
Let’s have a look at the benefits and drawbacks of both of these processes.
Benefits
- Deterministic models get the advantage of being simple.
- Deterministic is simpler to grasp and hence may be more suitable for some cases.
- Stochastic models provide a variety of possible outcomes and the relative likelihood of each.
- The Stochastic model uses the commonest approach for getting the outcomes.
Drawbacks
- In the deterministic approach, there are no cumulative probabilities due to which low reserve cases are overoptimistic.
- In the stochastic approach, the model is more complex, also called the black-box approach.
- The biases may be hidden in the stochastic model and it focuses on extremes.
Applications of Deterministic and Stochastic algorithms
- Deterministic models are used in the analysis of flood risk.
- The deterministic model used in the Turing machine is a machine (automaton) capable of enumerating any arbitrary subset of acceptable alphabet strings; these strings are part of a recursively enumerable set. A Turing machine has an infinitely long tape on which to execute read and write operations.
- Stochastic investing models aim to estimate price changes, returns on assets (ROA), and asset classes (such as bonds and equities) across time. It uses Monte Carlo simulation, which may simulate how a portfolio would perform based on the probability distributions of individual stock returns.
- Stochastic modelling influences the marketing and shifting movement of audience tastes and preferences, as well as the solicitation and scientific appeal of specific motion picture cameos (i.e., opening weekends, word-of-mouth, top-of-mind knowledge among surveyed groups, star name recognition, and other elements of social media outreach and advertising).
Conclusion
A deterministic approach has a simple and comprehensible structure which could be applied only when the relationship between variables is determined; on the other hand, a stochastic approach has a complex and incomprehensible structure which works on the likelihood of probabilities. With this article, we have understood the difference between the deterministic and stochastic approaches in machine learning.





















