With so many sectors making use of deep learning, the driving force — algorithms have to be efficient for the neural networks to learn faster and achieve better results. Optimisation techniques become the centrepiece of deep learning algorithms when one expects better and faster results from the neural networks, and the choice between these optimisation algorithms techniques can make a huge difference between waiting for hours or days for excellent accuracy. 

With limitless applications and a wide variety of researched topics on optimisation algorithms, here we highlight a few essential points taken from a well-written paper.

Gradient Descent

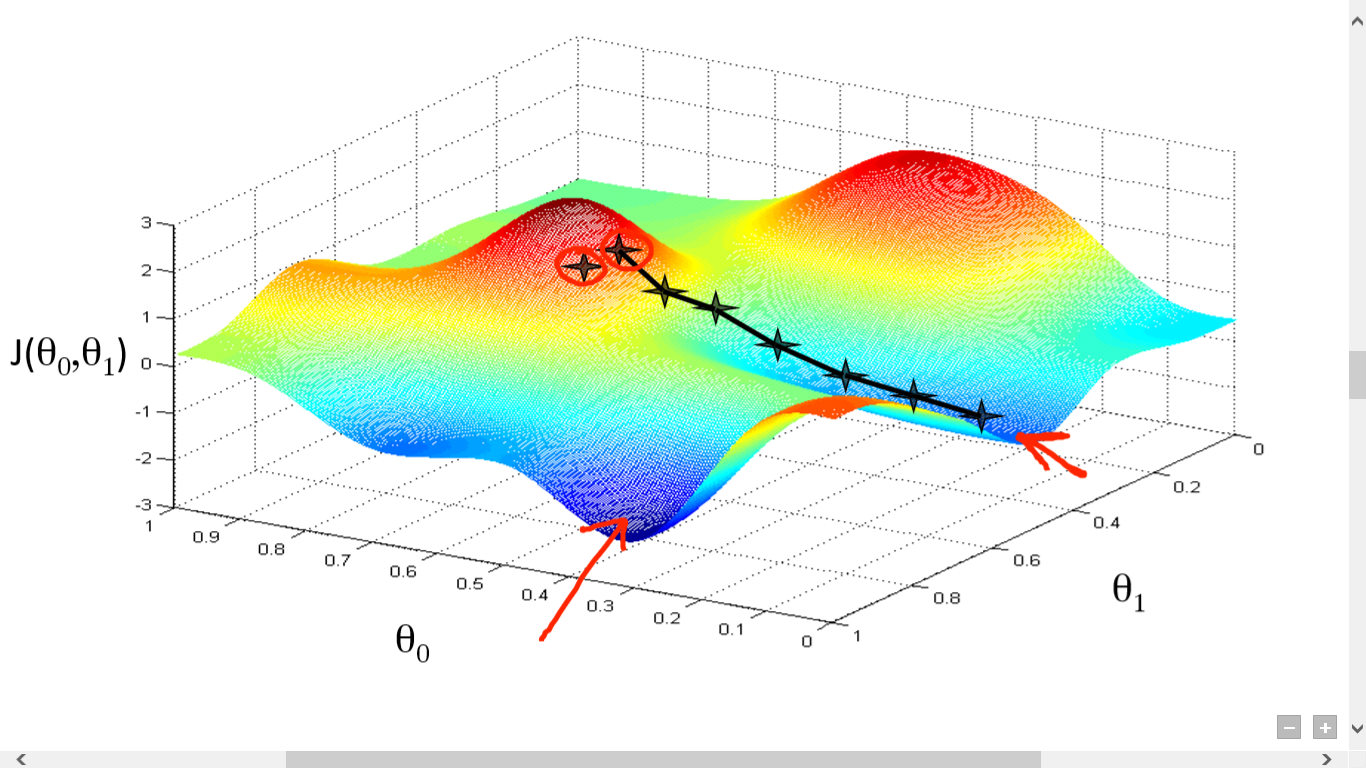
If one had to explain gradient descent in simple words, it is a process of training the neural network so that the difference between the desired value and the output is minimum. Gradient descent, aka backpropagation, involves two steps, firstly, calculating the loss function and secondly, updating the parameters in response to the gradients, and this is how the descent is done. This cycle is then repeated until one gets the minimum loss function. 

Let’s discuss the gradient computation by backpropagation and convergence analysis for this Gradient Descent (GD).

Backpropagation

Backprop is an abbreviation for “backward propagation of errors”. It is used in conjunction with gradient descent which means the practical implementation of the gradient computation. Backpropagation (BP) was an important finding in the history of neural networks.

This method calculates the gradient loss function taking weights in the network into account. This gradient is fed to the optimisation method, which updates the weights of the existing ones to minimise the loss function. Backpropagation has been used to calculate the loss function and to do that it requires a known output or the desired output for each input value. 

Backpropagation has found its applications in areas like classification problems, function approximation, time-space approximation, time-series prediction, face recognition, ALVINN- Enhancing training, etc.

Convergence Theorem

A neural network model in which each neuron performs a threshold logic function, the model always converges to a state of stability while operating in a serial mode and to a cycle of the length of the two while operating in full parallel mode. So, there are mainly two types of convergence results for gradient descent. If all the iterates are bounded, then GD with a proper constant step size converges.

There are many types of convergence theorems, like perceptron convergence theorem — a multi-layered convergence theorem also known as neural network; convergence theory for deep learning via over-parameterisation; and convergence results for neural networks via electrodynamics etc.

Learning Rate

For a neural network optimisation, there are all but two goals, one is to converge faster, and the other one is to improve a particular metric of interest. A faster method doesn’t generalise better and doesn’t really enhance the metric of interest, which is different from optimisation loss. Due to this, one has to try optimising idea in order to improve the convergence speed and accept that idea only if it passes a specific ‘performance check’.

The learning rate is a tuning parameter in an optimisation algorithm that is responsible for determining the step size at each iteration while moving towards a minimum function loss. It represents the speed at which a machine learning model learns since it influences the amount of old information which is vetoed by the newly acquired knowledge. 

The learning rate is denoted by η or α.

A learning rate schedule also keeps changing the step size during learning and changes between iterations/epochs, mainly done with two parameters: decay and momentum. The other types are time-based, step-based and exponential.

Initialisation

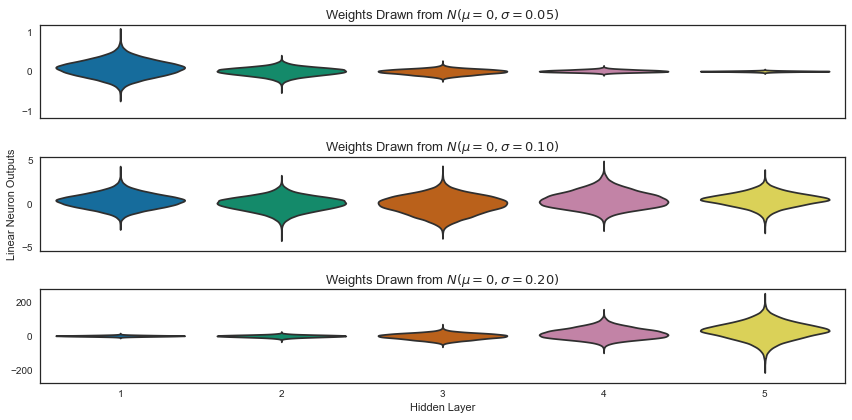
The initialisation is one of the significant tricks for training deep neural networks. Because of the exploding gradients or vanishing gradient regions, there exists a large portion of the whole space, and initialising in these regions will fail an algorithm. Thus this makes it ideal for picking the initial point in an excellent region to start with.

Types of initialisation:

• Naive initialisation: The suitable region to pick the initial point is unknown, so the first step is to find a simple initial point. One choice is the all-zero initial point, and the other one is a sparse initial point that is only a small portion of the weights which are non-zero or drawing weights end up forming certain random distribution.
• LeCun initialisation and Xavier initialisation which is designed for sigmoid activation functions.
• Kaiming initialisation for ReLU activation.
• Layered-Sequential Unit-Variance (LSUV), which shows empirical benefits for some problems.

Normalisation

Normalisation can be viewed as the extension to initialisation, so instead of merely modifying the initial point, this method changes the network for all the next iterates that follow.

Batch Normalisation is again a standard technique in today’s time. It reduces the covariance shift. Covariance shift happens is when an algorithm has learned X to Y mapping, then if the distribution of X changes, then the model has to be retrained. Another thing about BatchNorm can do is allowing each layer of a network to learn by itself independent of other layers.

The benefit of BatchNorm is to allow larger learning rate. The networks which do not have BatchNorm have larger isolated eigenvalues, while those with BatchNorm have no such issues with isolated eigenvalues.

BatchNorm, however, does not work very well with mini-batches which do not have similar statistics because the mean/variance for each mini-batch is computed as an approximation of the mean /variance for all samples. So researches have also proposed other normalisation techniques such as weight normalisation, group normalisation, instance normalisation, switchable normalisation and spectral normalisation.

Outlook

The optimisation of an algorithm has become an essential part of deep learning. It starts by defining a loss function and ends with minimising the loss function using one or the other optimisation routine. There are several optimisation algorithms out there like Stochastic Gradient Descent (SGD), RMSProp Optimisation, and Adam. 

In today’s times the more you know about the optimisation techniques, the more efficient your algorithms and neural networks will become. Nowadays, with so many new technologies being introduced, it becomes imperative that every developer know optimisation algorithms because optimisation offers more scalability, less processing time, and save memory.