ODE2VAE, a representation learning model, achieves state-of-the-art performance in long-term motion prediction and imputation tasks. It is introduced as a generative latent second-order Ordinary Differential Equation model for high dimensional sequential data such as motion capture. Variational autoencoders (VAE) are well known for their ability to extract hidden patterns from image data. VAE based models or their extensions usually assume static data. Hence VAE is not suitably applicable to sequential data, which are dynamic. ODE2VAE is a breakthrough in applying VAE to sequential data with latent space controlled by a continuous-time probabilistic second order ODE.
The model proposes a second-order ODE that permits modelling the latent dynamic ODE state, which decomposes high dimensional space into positions and momentum. To handle the uncertainty in the dynamics, the Bayesian neural network is introduced to the dynamics model. ODE2VAE performs state-of-the-art performance in all levels of learning with the variational inference approach, reproducing and forecasting high dimensional image sequential systems. Recurrent neural networks based VAE models can forecast a single step future image, but not a sequence of future images, whereas ODE2VAE predicts long-term future sequences with better accuracy than any of the well-known models.
First-order ODEs are incapable of modelling high-order dynamics such as acceleration or the motion of a pendulum. On the other hand, ODEs are deterministic systems unable to account for uncertainties in the dynamics. But ODE2VAE tackles both issues by introducing Bayesian neural second-order ODEs.
As a generative model, ODE2VAE consists of three components: first, the distribution of initial position and velocity; second, true dynamics defined by the acceleration field; third, a decoding likelihood.
Positional encoder maps the first example of high dimensional input sequence into a distribution of initial position in latent space. Velocity encoder maps a set of input sequence examples into a distribution of initial velocity in a latent space. Probabilistic latent dynamics are implemented by a second order ODE model parameterized by a Bayesian deep neural network. Data points in the original data domain are reconstructed by a decoder based on the parameters of time, position and velocity.
TensorFlow implementation of ODE2VAE
ODE2VAE is presently released as both TensorFlow implementation and PyTorch implementation. To obtain the package, we need to install the necessary libraries and dependencies with versions specified below.
%%bash pip install python==3.7 pip install tensorflow==1.13 pip install matplotlib pip install scipy pip install hickle==3.4 pip install tensorflow_probability
To run pre-trained model in our local machine,
%%bash git clone https://github.com/cagatayyildiz/ODE2VAE.git
We can verify the script files by providing the following command
!ls ODE2VAE/scripts
which gives an output of
To run the pre-trained bouncing balls script and its test script,
%%bash cd ODE2VAE ./scripts/train_bballs.sh ./scripts/test_bballs.sh
To run the pre-trained rotating mnist numbers script and its test script,
%%bash cd ODE2VAE ./scripts/train_mnist.sh ./scripts/test_mnist.sh
To run the pre-trained walking sequences script and its test script,
%%bash cd ODE2VAE ./scripts/train_mocap_single.sh ./scripts/test_mocap_single.sh
To run the pre-trained multiple-walking sequences script and its test script,
%%bash cd ODE2VAE ./scripts/train_mocap_many.sh ./scripts/test_mocap_many.sh
PyTorch Implementation of ODE2VAE
For PyTorch implementation, we need to install the following packages additionally,
%%bash pip install torch pip install torchdiffeq
Simple and complete python code implementation can be realized by importing the following libraries and modules.
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.parameter import Parameter
from torch.utils import data
from torch.distributions import MultivariateNormal, Normal, kl_divergence as kl
from torch_bnn import BNN
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
from torchdiffeq import odeint
import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt
plt.switch_backend('agg')
import os
os.environ['KMP_DUPLICATE_LIB_OK']='True'
from multiprocessing import Process, freeze_support
torch.multiprocessing.set_start_method('spawn', force="True")
Loading and Preprocessing of data can be done with
# prepare dataset
class Dataset(data.Dataset):
def __init__(self, Xtr):
self.Xtr = Xtr # N,16,784
def __len__(self):
return len(self.Xtr)
def __getitem__(self, idx):
return self.Xtr[idx]
# read data
X = loadmat('rot-mnist-3s.mat')['X'].squeeze() # (N, 16, 784)
N = 500
T = 16
Xtr = torch.tensor(X[:N],dtype=torch.float32).view([N,T,1,28,28])
Xtest = torch.tensor(X[N:],dtype=torch.float32).view([-1,T,1,28,28])
# Generators
params = {'batch_size': 25, 'shuffle': True, 'num_workers': 2}
trainset = Dataset(Xtr)
trainset = data.DataLoader(trainset, **params)
testset = Dataset(Xtest)
testset = data.DataLoader(testset, **params)
Define some useful classes to flatten and unflatten the views
class Flatten(nn.Module): def forward(self, input): return input.view(input.size(0), -1) class UnFlatten(nn.Module): def __init__(self,w): super().__init__() self.w = w def forward(self, input): nc = input[0].numel()//(self.w**2) return input.view(input.size(0), nc, self.w, self.w)
Finally, the VAE modelling class is developed with the code.
class ODE2VAE(nn.Module): def __init__(self, n_filt=8, q=8): super(ODE2VAE, self).__init__() h_dim = n_filt*4**3 # encoder output is [4*n_filt,4,4] # encoder self.encoder = nn.Sequential( nn.Conv2d(1, n_filt, kernel_size=5, stride=2, padding=(2,2)), # 14,14 nn.BatchNorm2d(n_filt), nn.ReLU(), nn.Conv2d(n_filt, n_filt*2, kernel_size=5, stride=2, padding=(2,2)), # 7,7 nn.BatchNorm2d(n_filt*2), nn.ReLU(), nn.Conv2d(n_filt*2, n_filt*4, kernel_size=5, stride=2, padding=(2,2)), nn.ReLU(), Flatten() ) self.fc1 = nn.Linear(h_dim, 2*q) self.fc2 = nn.Linear(h_dim, 2*q) self.fc3 = nn.Linear(q, h_dim) # differential function # to use a deterministic differential function, set bnn=False and self.beta=0.0 self.bnn = BNN(2*q, q, n_hid_layers=2, n_hidden=50, act='celu', layer_norm=True, bnn=True) # downweighting the BNN KL term is helpful if self.bnn is heavily overparameterized self.beta = 1.0 # 2*q/self.bnn.kl().numel() # decoder self.decoder = nn.Sequential( UnFlatten(4), nn.ConvTranspose2d(h_dim//16, n_filt*8, kernel_size=3, stride=1, padding=(0,0)), nn.BatchNorm2d(n_filt*8), nn.ReLU(), nn.ConvTranspose2d(n_filt*8, n_filt*4, kernel_size=5, stride=2, padding=(1,1)), nn.BatchNorm2d(n_filt*4), nn.ReLU(), nn.ConvTranspose2d(n_filt*4, n_filt*2, kernel_size=5, stride=2, padding=(1,1), output_padding=(1,1)), nn.BatchNorm2d(n_filt*2), nn.ReLU(), nn.ConvTranspose2d(n_filt*2, 1, kernel_size=5, stride=1, padding=(2,2)), nn.Sigmoid(), ) self._zero_mean = torch.zeros(2*q).to(device) self._eye_covar = torch.eye(2*q).to(device) self.mvn = MultivariateNormal(self._zero_mean, self._eye_covar) def ODE2VAE_rhs(self,t,vs_logp,f): vs, logp = vs_logp # N,2q & N q = vs.shape[1]//2 dv = f(vs) # N,q ds = vs[:,:q] # N,q dvs = torch.cat([dv,ds],1) # N,2q ddvi_dvi = torch.stack( [torch.autograd.grad(dv[:,i],vs,torch.ones_like(dv[:,i]), retain_graph=True,create_graph=True)[0].contiguous()[:,i] for i in range(q)],1) # N,q --> df(x)_i/dx_i, i=1..q tr_ddvi_dvi = torch.sum(ddvi_dvi,1) # N return (dvs,-tr_ddvi_dvi) def elbo(self, qz_m, qz_logv, zode_L, logpL, X, XrecL, Ndata, qz_enc_m=None, qz_enc_logv=None): [N,T,nc,d,d] = X.shape L = zode_L.shape[0] q = qz_m.shape[1]//2 # prior log_pzt = self.mvn.log_prob(zode_L.contiguous().view([L*N*T,2*q])) # L*N*T log_pzt = log_pzt.view([L,N,T]) # L,N,T kl_zt = logpL - log_pzt # L,N,T kl_z = kl_zt.sum(2).mean(0) # N kl_w = self.bnn.kl().sum() # likelihood XL = X.repeat([L,1,1,1,1,1]) # L,N,T,nc,d,d lhood_L = torch.log(1e-3+XrecL)*XL + torch.log(1e-3+1-XrecL)*(1-XL) # L,N,T,nc,d,d lhood = lhood_L.sum([2,3,4,5]).mean(0) # N if qz_enc_m is not None: # instant encoding qz_enc_mL = qz_enc_m.repeat([L,1]) # L*N*T,2*q qz_enc_logvL = qz_enc_logv.repeat([L,1]) # L*N*T,2*q mean_ = qz_enc_mL.contiguous().view(-1) # L*N*T*2*q std_ = 1e-3+qz_enc_logvL.exp().contiguous().view(-1) # L*N*T*2*q qenc_zt_ode = Normal(mean_,std_).log_prob(zode_L.contiguous().view(-1)).view([L,N,T,2*q]) qenc_zt_ode = qenc_zt_ode.sum([3]) # L,N,T inst_enc_KL = logpL - qenc_zt_ode inst_enc_KL = inst_enc_KL.sum(2).mean(0) # N return Ndata*lhood.mean(), Ndata*kl_z.mean(), kl_w, Ndata*inst_enc_KL.mean() else: return Ndata*lhood.mean(), Ndata*kl_z.mean(), kl_w def forward(self, X, Ndata, L=1, inst_enc=False, method='dopri5', dt=0.1): # encode [N,T,nc,d,d] = X.shape h = self.encoder(X[:,0]) qz0_m, qz0_logv = self.fc1(h), self.fc2(h) # N,2q & N,2q q = qz0_m.shape[1]//2 # latent samples eps = torch.randn_like(qz0_m) # N,2q z0 = qz0_m + eps*torch.exp(qz0_logv) # N,2q logp0 = self.mvn.log_prob(eps) # N # ODE t = dt * torch.arange(T,dtype=torch.float).to(z0.device) ztL = [] logpL = [] # sample L trajectories for l in range(L): f = self.bnn.draw_f() # draw a differential function oderhs = lambda t,vs: self.ODE2VAE_rhs(t,vs,f) # make the ODE forward function zt,logp = odeint(oderhs,(z0,logp0),t,method=method) # T,N,2q & T,N ztL.append(zt.permute([1,0,2]).unsqueeze(0)) # 1,N,T,2q logpL.append(logp.permute([1,0]).unsqueeze(0)) # 1,N,T ztL = torch.cat(ztL,0) # L,N,T,2q logpL = torch.cat(logpL) # L,N,T # decode st_muL = ztL[:,:,:,q:] # L,N,T,q s = self.fc3(st_muL.contiguous().view([L*N*T,q]) ) # L*N*T,h_dim Xrec = self.decoder(s) # L*N*T,nc,d,d Xrec = Xrec.view([L,N,T,nc,d,d]) # L,N,T,nc,d,d # likelihood and elbo if inst_enc: h = self.encoder(X.contiguous().view([N*T,nc,d,d])) qz_enc_m, qz_enc_logv = self.fc1(h), self.fc2(h) # N*T,2q & N*T,2q lhood, kl_z, kl_w, inst_KL = \ self.elbo(qz0_m, qz0_logv, ztL, logpL, X, Xrec, Ndata, qz_enc_m, qz_enc_logv) elbo = lhood - kl_z - inst_KL - self.beta*kl_w else: lhood, kl_z, kl_w = self.elbo(qz0_m, qz0_logv, ztL, logpL, X, Xrec, Ndata) elbo = lhood - kl_z - self.beta*kl_w return Xrec, qz0_m, qz0_logv, ztL, elbo, lhood, kl_z, self.beta*kl_w def mean_rec(self, X, method='dopri5', dt=0.1): [N,T,nc,d,d] = X.shape # encode h = self.encoder(X[:,0]) qz0_m = self.fc1(h) # N,2q q = qz0_m.shape[1]//2 # ode def ODE2VAE_mean_rhs(t,vs,f): q = vs.shape[1]//2 dv = f(vs) # N,q ds = vs[:,:q] # N,q return torch.cat([dv,ds],1) # N,2q f = self.bnn.draw_f(mean=True) # use the mean differential function odef = lambda t,vs: ODE2VAE_mean_rhs(t,vs,f) # make the ODE forward function t = dt * torch.arange(T,dtype=torch.float).to(qz0_m.device) zt_mu = odeint(odef,qz0_m,t,method=method).permute([1,0,2]) # N,T,2q # decode st_mu = zt_mu[:,:,q:] # N,T,q s = self.fc3(st_mu.contiguous().view([N*T,q]) ) # N*T,q Xrec_mu = self.decoder(s) # N*T,nc,d,d Xrec_mu = Xrec_mu.view([N,T,nc,d,d]) # N,T,nc,d,d # error mse = torch.mean((Xrec_mu-X)**2) return Xrec_mu,mse # plotting def plot_rot_mnist(X, Xrec, show=False, fname='rot_mnist.png'): N = min(X.shape[0],10) Xnp = X.detach().cpu().numpy() Xrecnp = Xrec.detach().cpu().numpy() T = X.shape[1] plt.figure(2,(T,3*N)) for i in range(N): for t in range(T): plt.subplot(2*N,T,i*T*2+t+1) plt.imshow(np.reshape(Xnp[i,t],[28,28]), cmap='gray') plt.xticks([]); plt.yticks([]) for t in range(T): plt.subplot(2*N,T,i*T*2+t+T+1) plt.imshow(np.reshape(Xrecnp[i,t],[28,28]), cmap='gray') plt.xticks([]); plt.yticks([]) plt.savefig(fname) if show is False: plt.close()
# calling the program to run
if __name__ == '__main__':
freeze_support()
ODE2VAE = ODE2VAE(q=8,n_filt=16).to(device)
Nepoch = 500
optimizer = torch.optim.Adam(ODE2VAE.parameters(),lr=1e-3)
for ep in range(Nepoch):
L = 1 if ep<Nepoch//2 else 5 # increasing L as optimization proceeds is a good practice
for i,local_batch in enumerate(trainset):
minibatch = local_batch.to(device)
elbo, lhood, kl_z, kl_w = ODE2VAE(minibatch, len(trainset), L=L, inst_enc=True, method='rk4')[4:]
tr_loss = -elbo
optimizer.zero_grad()
tr_loss.backward()
optimizer.step()
print('Iter:{:<2d} lhood:{:8.2f} kl_z:{:<8.2f} kl_w:{:8.2f}'.\
format(i, lhood.item(), kl_z.item(), kl_w.item()))
with torch.set_grad_enabled(False):
for test_batch in testset:
test_batch = test_batch.to(device)
Xrec_mu, test_mse = ODE2VAE.mean_rec(test_batch, method='rk4')
plot_rot_mnist(test_batch, Xrec_mu, False, fname='rot_mnist.png')
torch.save(ODE2VAE.state_dict(), 'ODE2VAE_mnist.pth')
break
print('Epoch:{:4d}/{:4d} tr_elbo:{:8.2f} test_mse:{:5.3f}\n'.format(ep, Nepoch, tr_loss.item(), test_mse.item()))
It is advisable to train or evaluate the CUDA GPU runtime implementations, though the code can be run in CPU runtime.
Performance evaluation
With the rotating mnist digits dataset, ODE2VAE can reconstruct the sequence of rotating images of digits with great performance.
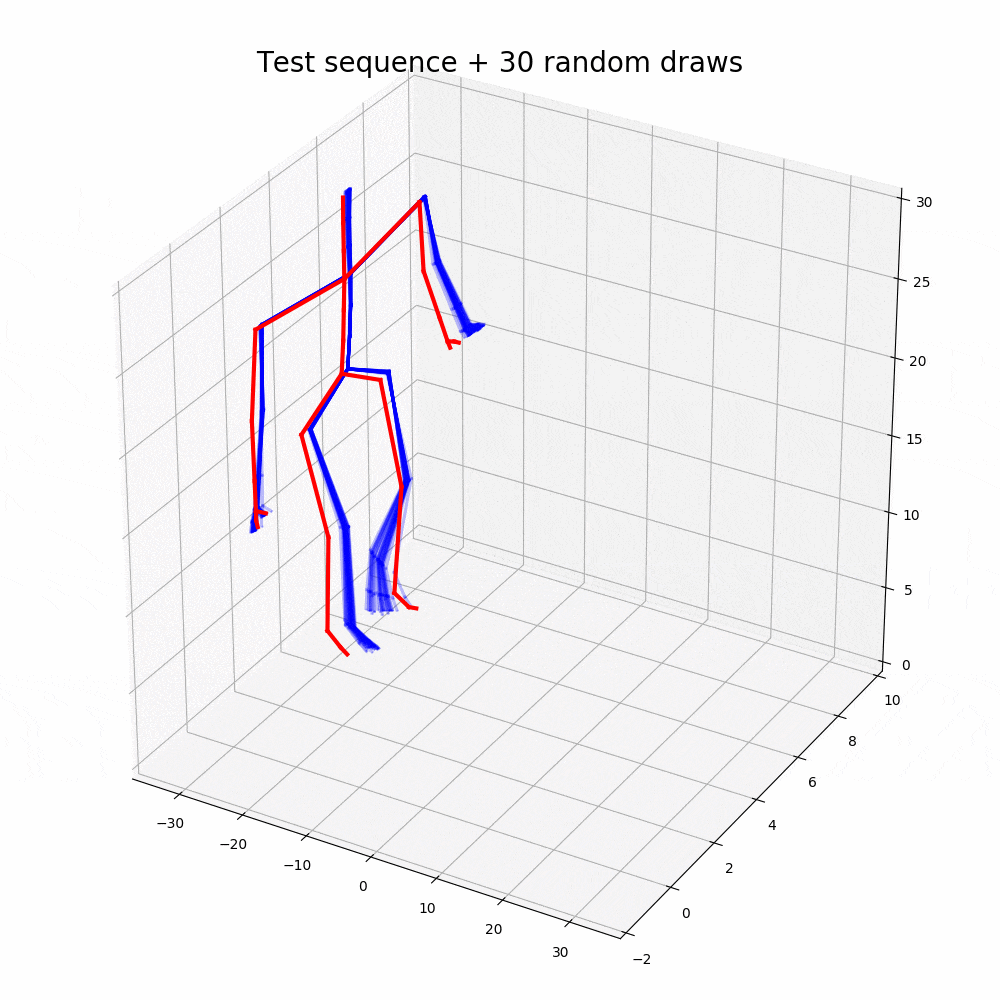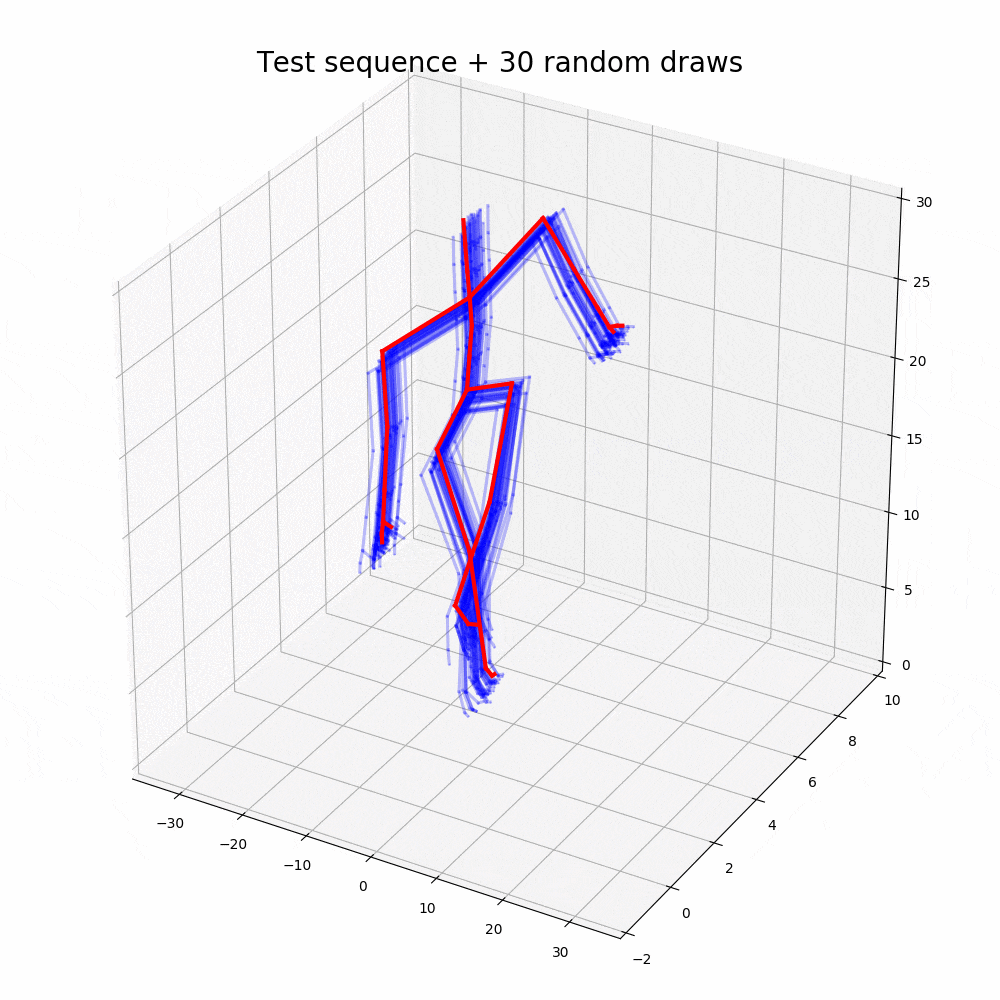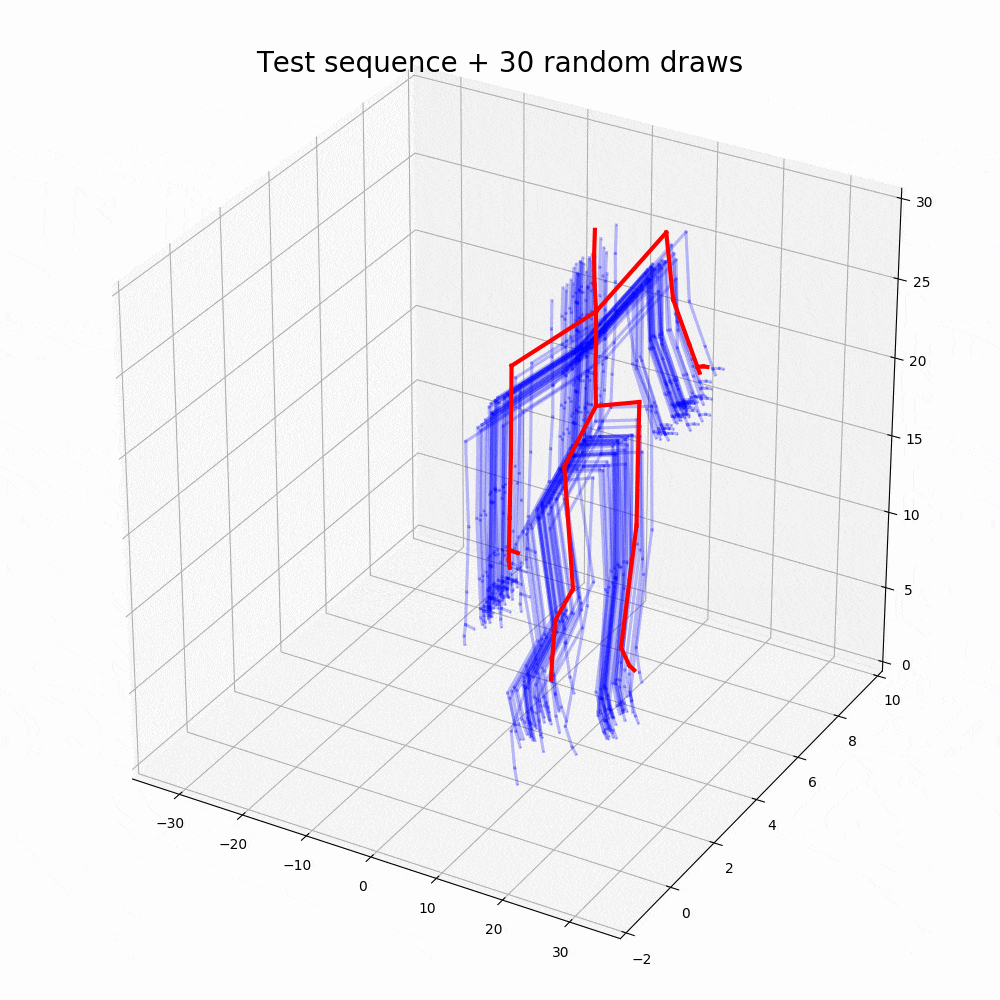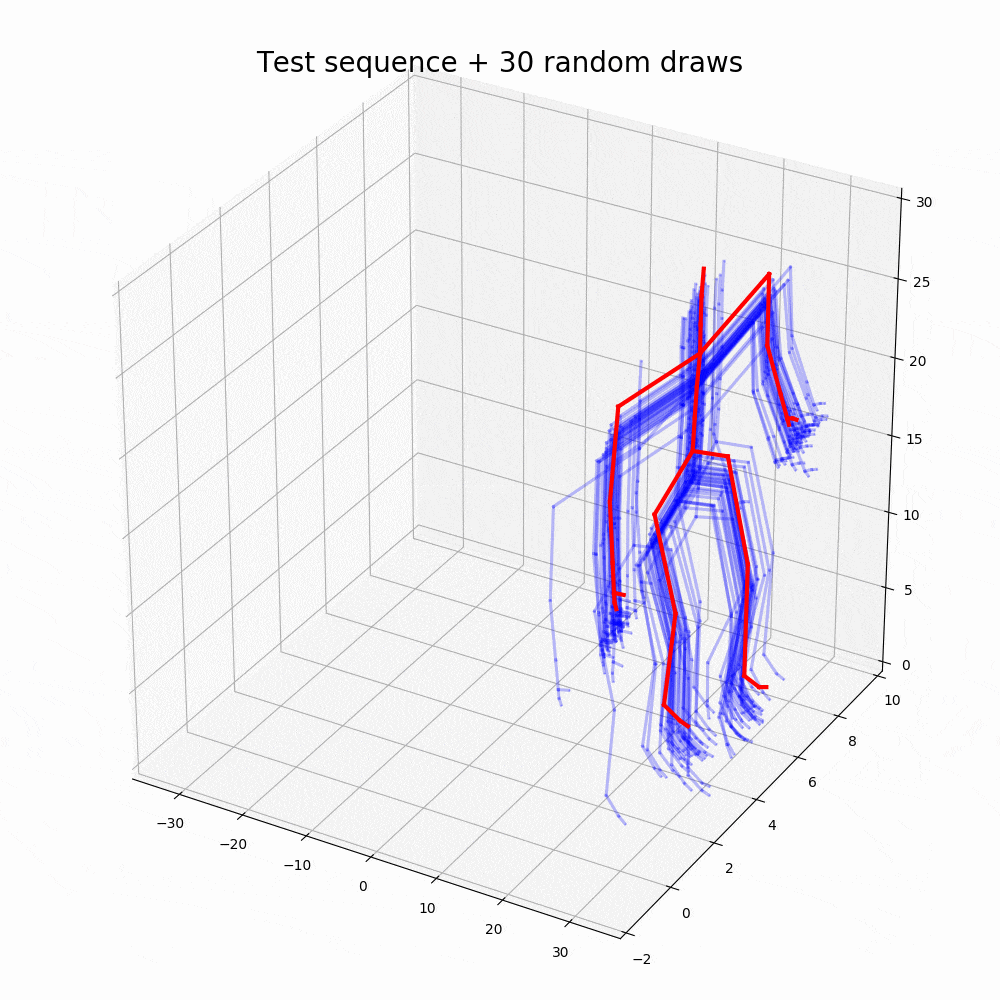
With the walking sequences dataset, the model can reconstruct the sequence with greater performance than any other representation learning algorithm.
Based on the performance, it is clear that the ODE2VAE outperforms any of the models in sequence reconstruction such as Gaussian Process Dynamic Models (GPDM), Variational Gaussian Process Dynamical Systems (VGPLVM), Deep Temporal Sigmoidal Belief Networks for Sequence Modeling (DTSBN-S), Gaussian Process Ordinary Differential Equation (npODE), Neural Ordinary Differential Equations (NeuralODE).
Note: Illustrations other than code outputs are obtained from the original research paper, corresponding github repository and public datasets.