If you are into the domain of building predictive models using machine learning then you might have come across a situation when your models perform very good on the training data and not so good on testing. This happens when the dataset is much complex like in Neural Networks. This problem of not generalization well in testing data is called Overfitting of the model.
It occurs when the error rate of a model is higher in testing as compared to training. What to do in these situations? Regularization is a technique that can help in these cases by adding some more information. It is also called Shrinkage Methods. Regularization techniques like Lasso Regression and Ridge Regression are used to avoid overfitting. The main idea behind regularization is to decrease the variance and increase bias a bit.
In this article, we will explore both the methods of regularization and check the results if we get rid of the overfitting situation. For this, we will use the Boston House Dataset where we will predict the prices of the house. The data set can be downloaded from Kaggle where it is publicly available.
What we will learn from this article?
- Overfitting of the Model
- Regularization
- Ridge Regression
- Lasso Regression
- Polynomial Models
Ridge Regression
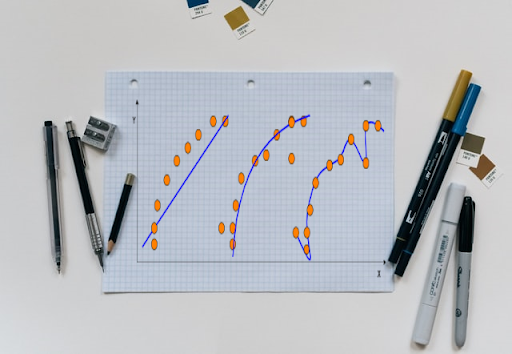
It is also called an L2 regularization that is used to get rid of overfitting. The goal while building a machine learning model is to develop a model that can generalize patterns well in training as well as in testing. Refer to the below graph that shows the best fit line for training and testing data. The line is perfect for the training data points that means the sum of residual is equal to 0 whereas the sum of residual for testing is high. This is termed as Overfitted model.
Ridge Regression is done to improve the generalizability of the model. This is done by tweaking the slope of the best fit line. Maybe the model does not perform much well in the training because now the line does not pass exactly to the data points but it will give fairly good results in testing. The slope is changed or the line is titled a bit by making use of the penalty term called Alpha which is a hyperparameter. Linear regression aims to reduce the sum of squared errors whereas in ridge regression it also reduces the sum of squared error but adds this penalty term by multiplying it with slope square. Check below for the graphical representation of the best fit line using ridge regression.
Linear regression = min(Sum of squared errors)
Ridge regression = min(Sum of squared errors + alpha * slope)square)
As the value of alpha increases, the lines gets horizontal and slope reduces as shown in the below graph.
Lasso Regression
It is also called as l1 regularization. Similar to ridge regression, lasso regression also works in a similar fashion the only difference is of the penalty term. In ridge, we multiply it by slope and take the square whereas in lasso we just multiply the alpha with absolute of slope.
Lasso Regression = min(sum of squared error + alpha * | slope| )
Similar to ridge regression as you increase the value of the penalty term the slope will get reduced and the line will become horizontal. As this term is increased it becomes less responsive to the independent variable.
Let us now practically see both the regularization techniques with implementing a regression model for Boston Housing Dataset.
First, we will import all the required libraries and the data set. After importing we will explore a bit data like shape and about missing values present in the data set. Use the below code to do the same.
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
df = pd.read_csv('Boston.csv')
print(df)
Output:
print(df.shape)
print(df.isnull().sum())
Output:
The data set contains 506 rows and 15 columns. There are no missing values that are found in the data. We will not divide the dependent variable and independent variable X and y respectively followed by scaling the data and then dividing it into training and testing sets. Use the below code to do so.
X = df.drop('medv', axis=1)
y = df['medv']
from sklearn import preprocessing
X = preprocessing.scale(X)
y = preprocessing.scale(y)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=1)
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
Output:
There are a total of 354 rows in the training data set and 152 are present in the testing data. We now build three models using simple linear regression, ridge regression and lasso regression and fit the data for training. After the model gets trained we will compute the scores for testing and training. Use the below code for the same.
regression_model = LinearRegression()
regression_model.fit(X_train, y_train)
ridge = Ridge(alpha=.3)
ridge.fit(X_train,y_train)
print ("Ridge model:", (ridge.coef_))
Output:
lasso = Lasso(alpha=0.1)
lasso.fit(X_train,y_train)
print ("Lasso model:", (lasso.coef_))
Output:
print("Linear Regression Model Training Score: ", regression_model.score(X_train, y_train))
print("Linear Regression Model Testing Score: ",regression_model.score(X_test, y_test))
print("Ridge Regression Model Training Score: ",ridge.score(X_train, y_train))
print("Ridge Regression Model Testing Score: ",ridge.score(X_test, y_test))
print("Lasso Regression Model Training Score: ",lasso.score(X_train, y_train))
print("Lasso Regression Model Testing Score: ",lasso.score(X_test, y_test))
Output:
The results are almost identical but with less complexity of the models. We will now create a polynomial regression model by creating new features from the features followed by transforming the data and dividing it into training and testing. Use the below code to do so.
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree = 2, interaction_only=True)
X_poly = poly.fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X_poly, y, test_size=0.30, random_state=1)
regression_model.fit(X_train, y_train)
print(regression_model.coef_[0])
Output:
ridge = Ridge(alpha=.3)
ridge.fit(X_train,y_train)
print ("Ridge model:", (ridge.coef_))
Output:
lasso = Lasso(alpha=0.003)
lasso.fit(X_train,y_train)
print ("Lasso model:", (lasso.coef_))
Output:
We will now check the scores of the polynomial model and compute the training and testing scores. Use the below code to do so.
print("Linear Regression Model Training Score: ", regression_model.score(X_train, y_train))
print("Linear Regression Model Testing Score: ",regression_model.score(X_test, y_test))
print("Ridge Regression Model Training Score: ",ridge.score(X_train, y_train))
print("Ridge Regression Model Testing Score: ",ridge.score(X_test, y_test))
print("Lasso Regression Model Training Score: ",lasso.score(X_train, y_train))
print("Lasso Regression Model Testing Score: ",lasso.score(X_test, y_test))
Conclusion
Regularization is done to control the performance of the model and to avoid the model to get overfitted. In this article, we discussed the overfitting of the model and two well-known regularization techniques that are Lasso and Ridge Regression. Lasso regression transforms the coefficient values to 0 which means it can be used as a feature selection method and also dimensionality reduction technique. The feature whose coefficient becomes equal to 0 is less important in predicting the target variable and hence it can be dropped. Ridge regression transforms the coefficient values to close to 0 and not completely equal to 0. You can also explore more about Ridge and Lasso here in this article titled “Ridge Regression Vs Lasso Regression”.