Many classical classification algorithms work straightforward when the data is linearly separable. But when this algorithm has to work on the data that is not linearly separable, it has to use a different strategy. Kernels are used by classification algorithms to solve non-linear classification problems. We mostly refer to the kernel used in the Support Vector Machine (SVM) algorithm. Keeping it as a reference point, in this post, we will discuss in detail the kernel used to learn non-linear functions used to map the non-linear relationship between two variables. We will go through this approach and understand it with examples. We will also discuss the kernel tricks and different kernel functions used in machine learning. The major points to be discussed in this article are outlined below.
Table of Contents
- Need of the Kernel
- How Does a Kernel Work?
- The Kernel Trick
- Types of Kernel Functions
Let’s start the discussion by knowing what the kernel actually is.
Need of the Kernel
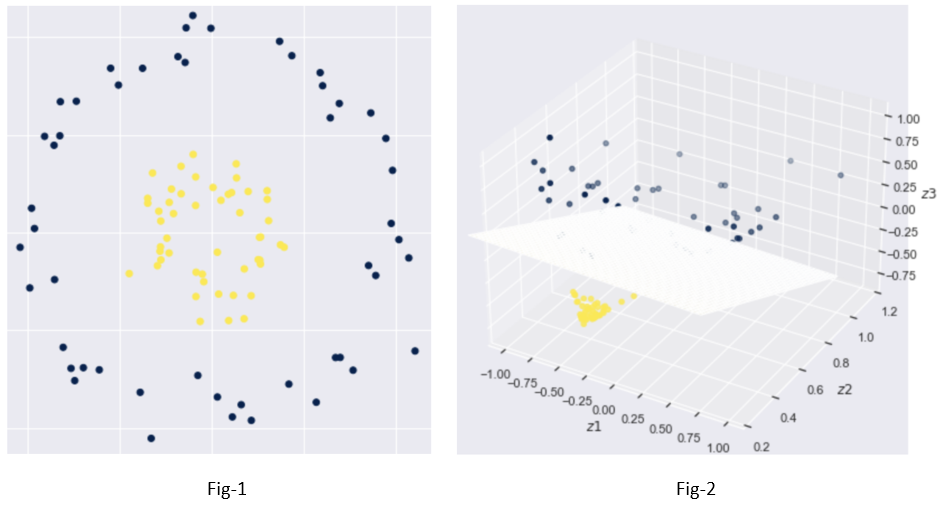
Let’s say we have a 2-dimensional dataset with two classes of observations, as illustrated in fig-1 below, we need to design a function to separate them. As it can be seen below that the given data in a 2-dimensional space is not linearly separable.
To segregate the data, we’d have to fit a function, which complicates our categorization challenge. But what if we could translate this data into a higher-dimensional (3D) space where a linear classifier could separate the data?
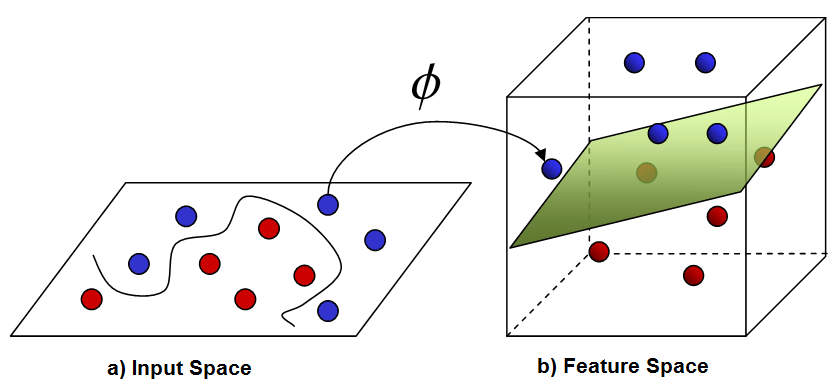
We can find a mapping from 2D to 3D space that allows us to linearly separate our observations, transform our two-dimensional data into three-dimensional data, help to find a linear decision boundary, fit a linear classifier (a plane dividing the data shown in fig-2) in 3D space.
This is when the kernel technique comes in handy. The goal is to use a function that projects / transform the data in such a way that it can be separated linearly. By using the maximum margin in the SVM method, data becomes linearly separable.
How Does a Kernel Work?
Kernel machines are a class of pattern-analysis algorithms, the most well-known member of which is the support vector machine (SVM). The general objective of pattern analysis is to discover and investigate various sorts of relationships (for example, clusters, ranks, principal components, correlations, and classifications) in datasets. Many algorithms that solve these tasks require the data in raw representation to be explicitly transformed into feature vector representations via a user-specified feature map: kernel methods, on the other hand, require only a user-specified kernel, i.e., a similarity function over pairs of raw data points.
Kernel methods are approaches for dealing with linearly inseparable data or non-linear data sets like those presented in fig-1. The concept is to use a mapping function to project nonlinear combinations of the original features onto a higher-dimensional space, where the data becomes linearly separable. The two-dimensional dataset (X1, X2) is projected into a new three-dimensional feature space (Z1, Z2, Z3) in the diagram above, where the classes become separable.
To grasp it completely, Assume we have two vectors, x and x*, in a 2D space (illustrated in fig-1) and want to find a linear classifier by performing a dot product between them. Unfortunately, in our current 2D vector space, the data is not linearly separable. We can address this challenge by mapping the two vectors to a 3D space.
x→ϕ(x)
x∗→ϕ(x*)
Where (x) and (x*) are 3D representations of x and x*, respectively. Now we can discover our linear classifier in 3D space using the dot product of (x) and (x*) and then map back to 2D space using the dot product of (x) and (x*) like below.
xT x∗→ϕ(x)T ϕ(x∗)
A mapping function can be used to convert the training data into a higher-dimensional feature space, and then a linear SVM model can be trained to classify the data in this new feature space following the method outlined above. Using the mapping function, the new data may then be fed into the model for categorization. However, this method is computationally intensive. So, what is the solution?
The approach is to use a method to avoid explicitly mapping the input data to a high-dimensional feature space in order to train linear learning algorithms to learn a nonlinear function or decision boundary. This is known as a kernel trick. It should be noted that the kernel trick is significantly more general than SVM.
The Kernel Trick
We’ve seen how higher-dimensional transformations can help us separate data so that classification predictions can be made. It appears that we will have to operate on the higher dimensional vectors in the modified feature space in order to train a support vector classifier and maximize our objective function.
In real-world applications, data may contain numerous features, and transformations using multiple polynomial combinations of these features will result in extremely large and prohibitive processing costs.
This problem can be solved using the kernel trick. Instead of explicitly applying the transformations (x) and representing the data by these transformed coordinates in the higher dimensional feature space, kernel methods represent the data only through a set of pairwise similarity comparisons between the original data observations x (with the original coordinates in the lower dimensional space).
Our kernel function takes in lower-dimensional inputs and outputs the dot product of converted vectors in higher-dimensional space. Other theorems guarantee that such kernel functions exist under certain conditions.
If a function can be written as an inner product of a mapping function, we only need to know that function, not the mapping function, as shown above. A Kernel Function is a name for the function.
Types of Kernel Functions
The kernel function is a function that may be expressed as the dot product of the mapping function (kernel method) and looks like this,
K(xi,xj) = Ø(xi) . Ø(xj)
The kernel function simplifies the process of determining the mapping function. As a result, the kernel function in the altered space specifies the inner product. Different types of kernel functions are listed below. However, based on the requirement that the kernel function is symmetric, one can create their own kernel functions.
Polynomial Kernel
The polynomial kernel is a kernel function that allows the learning of non-linear models by representing the similarity of vectors (training samples) in a feature space over polynomials of the original variables. It is often used with support vector machines (SVMs) and other kernelized models.
F(x, xj) = (x.xj+1)^d
Sigmoid Kernel
It is primarily used in neural networks. This kernel function is similar to the activation function for neurons in a two-layer perceptron model of a neural network.
F(x, xj) = tanh(αxay + c)
Linear Kernel
It is the most fundamental sort of kernel and is usually one-dimensional in structure. When there are numerous characteristics, it proves to be the best function. The linear kernel is commonly used for text classification issues since most of these problems can be linearly split. Other functions are slower than linear kernel functions.
F(x, xj) = sum( x.xj)
Radial Basis Function (RBF) Kernel
The radial basis function kernel, often known as the RBF kernel, is a prominent kernel function that is utilized in a variety of kernelized learning techniques. It is most typically used in support vector machine classification. The RBF kernel is defined on two samples x and x’, which are represented as feature vectors in some input space, as
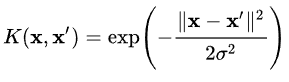
Conclusion
In this post, we have seen the importance of kernels when mapping nonlinear data. It is also referred to as a black-box kind of operation which is a bit confusing to understand for novices. From the very first point, we have identified the need for kernels in the non-linear domain. Later we understood what kernel operation actually is and to whom the kernel trick is referred. And lastly, we went through some popular kernels used under the SVM algorithm.