Convolutional Neural networks (CNNs) have a large number of variables and, as a result, are difficult to implement. Various methods and techniques, such as quantization and pruning, have been developed to address the issue of CNN complexity. Fourier domain computation is a new paradigm for the acceleration of CNNs among the various simplification methods. In this article, we will look at how the Fourier domain can be used to simulate the behaviour of CNN in terms of computational efficiencies, such as the Convolutional and Pooling operations. Below is a list of the main points to be discussed in this article.
Table of Contents
- Standard Convolutional Layer
- What is Fourier Transform?
- How Can Fast Fourier Convolution be Used?
- Fourier Convolutional Layer
- Fourier Padding Layer
Let’s start the discussion by understanding how standard CNN behaves and its drawbacks.
Standard Convolutional Layer
Convolutional Neural Network (CNN) is a popular, cutting-edge deep learning approach to computer vision that has a wide range of applications in domains where data may be represented by multi-dimensional matrices. In the case of the picture and video analysis, for example. CNN’s were first used on picture data for the tasks of handwriting recognition.
Since then, substantial recent advances in the availability of processing power have aided the practicality of CNNs and deep learning in general, in addition to theoretical advances. Graphics Processing Units (GPUs), for example, enable us to deal with the massive computing required by convolution.
The convolutional neural network (CNN) is the simplest basic neural network used in computer vision to tackle problems such as classification, segmentation, and denoising. One of the drawbacks of CNN training is that the convolution process for all convolutional layers is quite expensive. As the size of the image or kernel increases, so does the quantity of processing, resulting in learning lag.
Because convolution in the spatial domain is the same as pointwise multiplication in the Fourier domain, the one proposed solution is to change the domain using the Fourier transform and build a CNN in the frequency domain. Point-by-point multiplication is generally less complicated and less expensive to compute than convolution.
The Fourier Convolution Neural Network (FCNN) is a technique where just the Fourier domain is used for training. The effect is a significant reduction in training time while maintaining efficacy. The Fourier domain is used to analyze and represent images, and a convolution mechanism is utilized in a manner similar to that used in more traditional CNN algorithms.
Before proceeding to the technique directly, we first look at what is Fourier transform is.
What is Fourier Transform?
The Fourier transform (FT) decomposes functions based on space or time into functions based on spatial or temporal frequency, such as expressing a musical chord in terms of the volumes and frequencies of its constituent notes. The frequency-domain representation and the mathematical method that associates the frequency domain representation with a space or time function are referred to as the Fourier transform.
A function of time’s Fourier transform is a complex-valued function of frequency whose amplitude (absolute value) equals the amount of that frequency included in the original function and whose argument is the phase offset of the fundamental sinusoid at that frequency.
The Fourier transform is not restricted to time functions; however, the original function’s domain is generally referred to as the time domain. There is also an inverse Fourier transform, which uses the Fourier inversion theorem to theoretically reconstruct the original function from its frequency domain representation.
How Can Fast Fourier Convolution be Used?
The above-mentioned FCNN approach has the advantage of reducing complexity, especially in the context of larger images, and thus increasing network efficiency significantly. The Convolution Theorem’s basic notion, which claims that for two functions k and u, we have
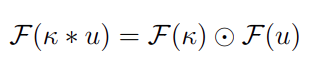
where F(.) stands for Fourier transform, * represents convolution, and the Hadamard Pointwise Product is shown by ๏. Fast Fourier Transforms can now be used to calculate convolution more efficiently (FFTs).
Because convolution corresponds to the Hadamard product in the Fourier domain, and given the efficiency of the Fourier transform, this method requires far fewer computational operations than the sliding kernel spatial method and is thus much faster. Working in the Fourier domain is more difficult because we can’t see the filters learned by our Fourier convolution; this is a common issue with CNN techniques.
Now further we will discuss how the main operations of a CNN layer, that is convolution and Pooling, can be carried out in the Fourier domain.
Fourier Convolutional Layer
The sliding window approach is used in traditional CNNs to perform discrete convolutions between images and kernel functions. In other words, a window the size of the kernel matrix is dragged across the image. The convolution is calculated by adding the Hadamard product of the image patch and the kernel.
In terms of the FCNN, we intend to replace the sliding window approach with the Fourier transform in the first instance, using the discrete analogue of the convolution theorem discussed above. The computation of the discrete Fourier transform for an image involves multiplications and additions, but this can be greatly reduced by using an FFT algorithm like Cooley-Tukey, which can compute the Direct Fourier Transform (DFT) with multiplications and additions. This results in an overall improvement from the operations required to calculate the DFT directly to those required for the FFT.
For larger images, this decrease in the number of operations results in an increasing relative speed-up. This is especially important now that larger computer vision (image) datasets are becoming more widely available. The advantage of Fourier convolutions is not only their speed but also the fact that we can pool data during the convolution phase to reduce computation costs.
Because they remain in the Fourier domain throughout, these convolution kernels can learn the equivalent of arbitrarily large spatial kernels limited only by initial image size. The image size is significantly larger than the size chosen by spatial kernels. That is, Fourier kernels that match the image size can learn a good representation of a 3 x 3 spatial kernel or a 5 x 5 spatial kernel, depending on which aids learning the most.
This is a general improvement to kernel learning in neural networks because most networks typically learn kernels of a fixed size, reducing the network’s ability to learn the optimal spatial kernel size. In the Fourier domain, we can train to find not only the optimal spatial kernel of a given size but also the optimal spatial kernel size and the optimal spatial kernel itself.
Fourier Padding Layer
The image data is distributed differently in the Fourier domain than it is in the spatial domain. This allows us to reduce the data size by the same amount as in the spatial domain while retaining more information.
High-frequency data is found near the centre of a Fourier matrix, while low-frequency data is found near the edges. As a result, it truncates the matrices’ boundaries because the high-frequency Fourier data contains more of the spatial information that it wishes to retain.
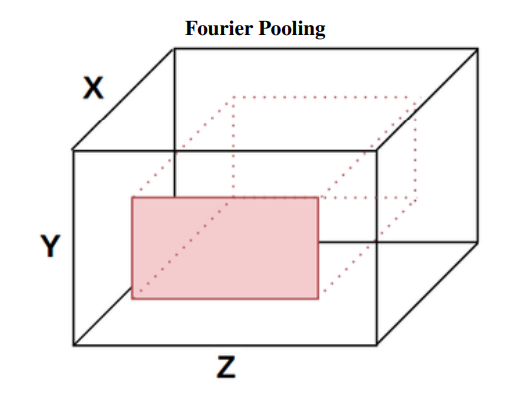
This Fourier pooling layer, depicted in the figure above, works as follows.
Given a complex three-dimensional tensor with X, Y, and Z dimensions and an arbitrary pool_size variable corresponding to the amount of data we want to keep.
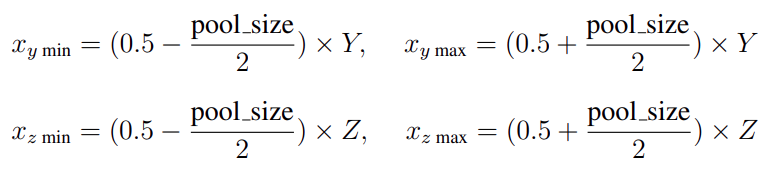
For our FCNN, this method provides a simple Fourier pooling layer. It only requires the GPU to perform a small number of computation operations during training. In the spatial context, max-pooling is the equivalent method, which takes the maximum value in a k x k window where k is a chosen parameter. If k = 2, for example, max-pooling reduces the data size by a quarter by taking the maximum value in each of the 2 x 2 matrices across the entire data set. Similarly, in our Fourier pooling, we would use pool size = 0.25 to reduce the size of the data even more.
Final Words
We discussed an efficient Fourier domain-based method for image convolutional operations. FCNNs are Fourier Convolution Neural Networks that provide run-time benefits, particularly during training. This approach can also be used to classify image sets with large images, which is not possible with spatial CNNs. We mainly discussed how a standard convolutional network performs the process and where it falls short, and we saw how the Fourier domain could be used to address the major issues that CNN faces in this post.