In recent years, we have seen the success of machine learning in various fields and with this, we have also witnessed the development involved in machine learning algorithms. Sometimes these algorithms are totally or partially based on mathematical operations and logic. Similarly, Boolean algebra is also a part of mathematics and mathematical logic that can be used in machine learning. In this article, we are going to discuss the application of Boolean algebra in machine learning. The major points to be discussed in part one of the article are listed below. 

Table of Contents

1. Why is Boolean algebra used in machine learning?
2. Related works: Boolean algebra in machine learning
3. Major applications in machine learning
4. Real-life applications

Let’s start the discussion by understanding why Boolean algebra is used in machine learning.

Why is Boolean algebra used in machine learning?

Boolean algebra is introduced in machine learning to overcome some of the drawbacks of this field. One of the major drawbacks is that machine learning algorithms are some kind of black-box technique. To understand it more we can take an example of a multiple layers perception network or support vector machines. Using these techniques, we can achieve good accuracy while modelling but when it comes to understanding the inner workings of the model we don’t get that much detail. On the other hand, algorithms like random forest and decision trees can describe the working but many times we don’t get good results. This drawback of black-box can be resolved using Boolean algebra. 

Also, this introduction of Boolean algebra in machine learning made use of Boolean algebra to build sets of intelligible rules able to obtain very good performance. The above-given example is just a basic application of Boolean algebra in machine learning. multilayer perceptrons. perceptron is an algorithm for supervised learning of binary classifiers.

As we know, Boolean algebra works on the logic and conditions of rules. A basic model that can contain Boolean algebra can work on the rules. For example, a basic model with Boolean algebra starts with the data with a target variable and input or learner variables and using the set of rules it generates output value by considering a given configuration of input samples. A simple rule can be written as:

If premise then consequences 

In the above rule, the premise contains one or many conditions on the input and the consequence contains an output value. Condition on the premises can have different forms according to the type of input:

• If variables are categorical then the input value must be in a subset,  

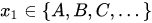
• If variables are ordered then the condition is written as inequality or an interval,

or

Therefore the possible rule can be written as follows:

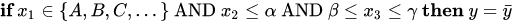
In the above expression, we have discussed a basic intuition behind why we need boolean algebra in machine learning. In the next section of the article, we will discuss the work which has been done based on this intuition. 

Related works: Boolean algebra in machine learning

In this section of the article, we mainly focus on the works where we can find boolean algebra in machine learning. Some of the work related to this are listed below:

• Switching Neural Networks: A New Connectionist Model for Classification: In this work, we can see an example of a model where boolean algebra is used with the layers of connectionist neural networks. In the architecture of this work, we find the first layer of the model is containing an A/D converter that transforms the input samples into binary strings, and then the next two layers of the network use a positive Boolean Function that solves in an A/D converter domain the original classification problem. The function used by the neural network in this work can be written in the form of intelligible rules.  A proper method for reconstructing the positive boolean function can be adapted to train the model. They have named the model Switching Neural Network. The image below is a representation of the schema of  Switching Neural Networks. 

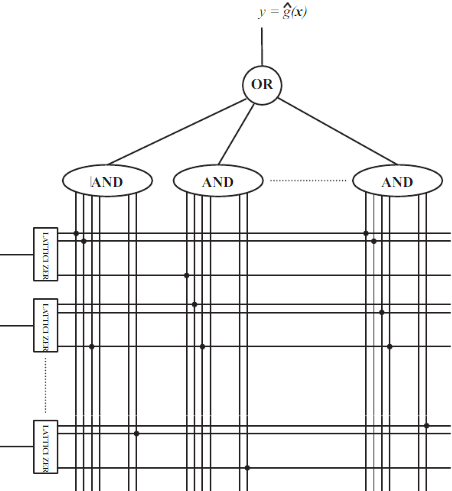
We can consider this work as a neural network with three feed-forward layers where the first one is used for binary mapping and the next two layers are used for expressing the positive boolean function. Every port in the second layer is connected only to some of the outputs leaving the latticizers.

• Learning Algorithms via Neural Logic Networks: This work is based on making a paradigm for neural networks to learn using the boolean neural network. Basic differential operators from the boolean system such as conjunction, disjunction, and exclusive-OR are used. These Basic differential operators can be combined with deep neural networks like MLP. This work can be a witness to overcoming some of the drawbacks of the MLP for learning discrete-algorithmic tasks. The model of this work is known as Neural Logic Network in which Neural Logic Layersbased on have been introduced using any boolean function. Types of these Neural Logic Layers are as follows: 

1. Neural conjunction layer: hold the conjunction function from boolean algebra.
2. Neural disjunction layer: holds the disjunction function from boolean algebra.
3. Neural XOR Layer: hold the XOR or exclusive OR function from boolean algebra.

The image below is a comparison of  MLP vs NLN for learning Boolean functions.

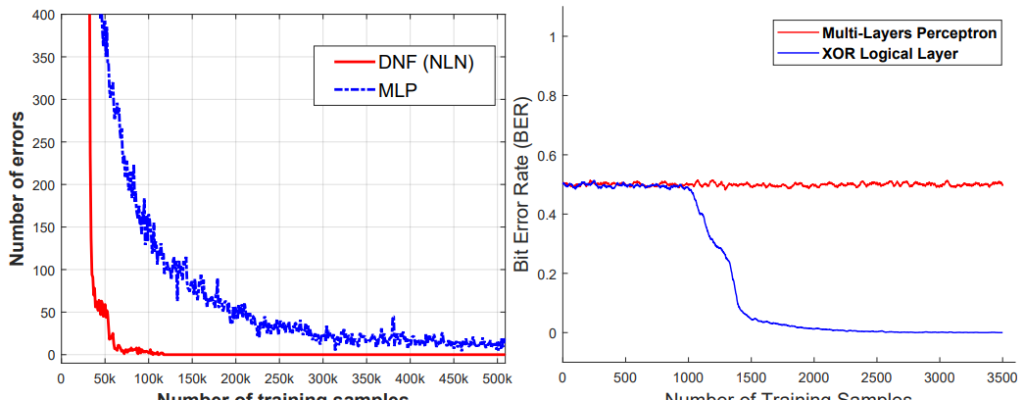
The above-given approaches are two basic works which after introduction have been updated and used in various real-life applications. In the next section of the article, we will discuss the real-life application of machine learning algorithms that are using Boolean algebra.

Major applications of Boolean algebra in machine learning

Some of the major applications of Boolean algebra in the field of machine learning are listed below:-

• Demonstration of Classification by a Perceptron: To demonstrate how perceptrons can classify the linearly separable patterns, the truth tables of Boolean AND or OR operations can be used. The results of the operations indicate the class labels while the input patterns represent the data points in the 2D space. 
• XOR Problem and Multilayer Perceptron: As discussed above, the perceptrons can classify the input patterns of Boolean AND or OR operations with a single-layer architecture. But they fail to classify the patterns of an XOR operation. To classify them correctly, lead the development of the multilayer perceptrons. 
• Different gates used in LSTM Recurrent Neural Network: We can see the usage of gates in the LSTM networks, especially in gates. We can take an example of a to forget gate where the result of the sigmoid function (i.e. the forget state) is an indicator of pointwise multiplication with the cell state that will cause the cell state to “forget all information” or “remember all information”. This can be completed using the concept of Gates based on boolean algebra.

Real-life applications

We can see the uses of this approach, i.e. machine learning with Boolean algebra,  in various fields like medicine, financial services, and supply chain management. In this section of the article, we will discuss some of the important and famous real-life applications that are listed below. 

• The work of the Switching neural network has been applied to medical science where it is used to classify the new multiple osteochondromas which is a type of tumour of the bones. More details about this application can be found here.
• This approach is applied to make a prognostic classifier for neuroblastoma patients. Neuroblastoma is a type of cancer that is mainly discovered in the small gland. In basic, this classifier consisted of 9 rules utilizing mainly two conditions of the relative expression of 11 probe sets and algorithm applied to microarray data and patients’ classification. We can find more details about the work here. 
• This approach has been applied to the diagnosis of pleural mesothelioma. For this purpose, they have applied the logic learning machine to a data set of 169 patients in northern Italy.  They have also compared the algorithm’s result with the results of other algorithms like decision trees, KNN, and artificial neural networks and found out the outperformance of switching neural networks. We can find more details about this work here.  

Final words 

In this article, we have discussed why we require Boolean algebra in machine learning with an intuition of how it can be applied in machine learning. Along with this, we have also discussed some of the major related works with their application in real life.