|
Listen to this story
|
The cost function in several machine learning algorithms is minimized using the optimization approach gradient descent. Its primary objective is to update the parameters of a learning algorithm. These models gain knowledge over time by using training data, and the cost function in gradient descent especially serves as a barometer by assessing the correctness of each iteration of parameter changes. Gradient descent is commonly used in supervised learning but the question is whether it could be used in Unsupervised Learning. This article will focus on understanding ‘how’ gradient descent could be used in unsupervised learning. Following are the topics to be discussed.
Table of contents
- About Gradient Descent
- Training word2vec models
- Training autoencoder models
- Training CNNs
Gradient Descent finds the global minima of a cost function, so it can’t be applied to algorithms without a cost function. Let’s start with a high-level understanding of gradient descent.
About Gradient Descent
Although the gradient descent algorithm is based on a convex function, but behaves similar to a linear regression algorithm, below is an example to refer to.
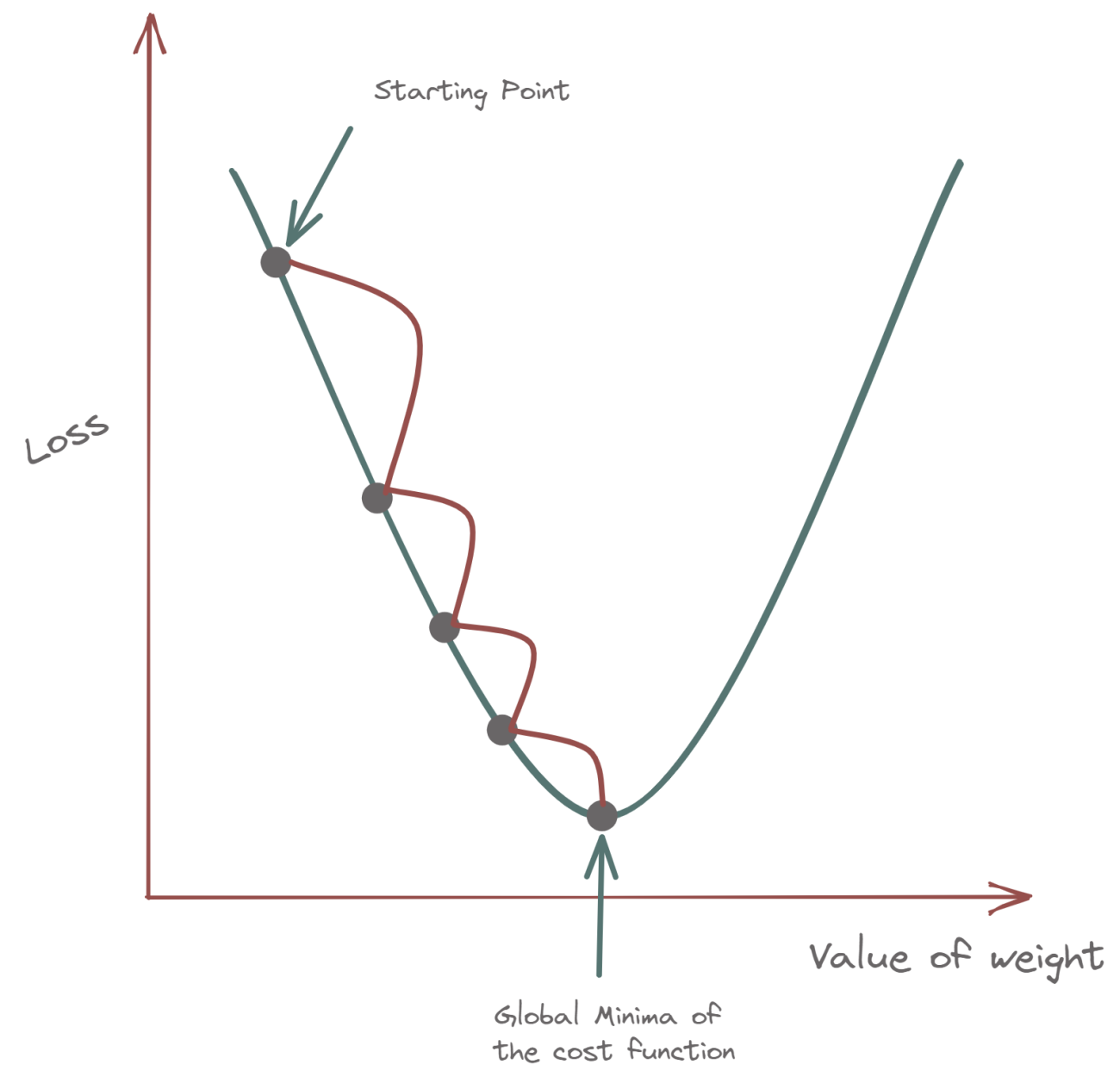
The beginning point is only a position chosen at random by the algorithm to gauge performance. A slope would be discovered from that starting point, and from there, a tangent line would be created to gauge the slope’s steepness. The modifications to the parameters, such as the weights and bias, will be informed by the slope. The slope will be steeper at the starting point, but when additional parameters are created, the steepness should steadily diminish until it hits the point of convergence, which is the lowest point on the curve.
The objective of gradient descent is to reduce the cost function, or the difference between the anticipated value and the actual value, much like finding the line of best fit in linear regression. Two data points, a direction and a learning rate are necessary. Future iterations might gradually approach the local or global minimum because these variables impact the partial derivative computations of those iterations.
- Learning rate: The magnitude of the steps needed to get to the minimum is referred to as the learning rate. This is usually a modest value, and it is assessed and updated in accordance with how the cost function behaves. Larger steps are taken as a result of high learning rates, due to which the minimum may be exceeded. A poor learning rate, on the other hand, has short step sizes. The number of repeats reduces overall efficiency even if it has the benefit of greater precision since it requires more time and calculations to get to the minimum.
- The cost function: It calculates the error between the actual y value and the expected y value at the present point. This increases the effectiveness of the machine learning model by giving it feedback so that it may change the parameters to reduce error and locate the local or global minimum. Up until the cost, the function is near to or equal to zero, it constantly iterates, travelling in the direction of the sharpest fall (or the negative gradient). The model will then stop learning at this moment.
In unsupervised learning there gradient descent could only be utilized in Neural networks because it has a cost function and other unsupervised learning doesn’t have a cost function which is needed to be optimized. Let’s apply the gradient descent algorithm to some unsupervised learning and learn the functionality of these unsupervised learners.
Are you looking for a complete repository of Python libraries used in data science, check out here.
Training word2vec models
Word2vec is a method for processing natural language. With the help of a huge text corpus, the word2vec technique employs a neural network model to learn word connections. It is a two-layer neural network that “vectorizes” words to analyze text. It takes a text corpus as input and produces a set of vectors as output. Words in the corpus are represented by feature vectors. Once trained, a model like this may identify terms that are similar or propose new words to complete a phrase. As the name suggests, word2vec uses a specific set of integers called a vector to represent each unique word. The vectors are chosen so that a straightforward mathematical function may be used to determine the similarity of the words represented by those vectors to one another in terms of meaning.
The word2vec model could be trained using two different algorithms which are skip-gram and CBOW (Continuous bag of words). The skip-gram algorithm is based on gradient descent optimization. When given a current word, the continuous skip-gram model learns by predicting the words that will be around it. To put it another way, the Continuous Skip-Gram Model foretells words that will appear before and after the present word in the same phrase within a specific range.
Finding the vector representation of each and every word in the text is the major goal since it decreases the dimensional space. Each word in a skip-gram will have two distinct representations as its trick. The representation is defined as:
- When the word is a centre word
- When the word is a context word
The target word or input delivered is w(t), as shown in the skip gramme architecture shown above. One hidden layer computes the dot product of the input vector and the weight matrix. In the buried layer, no activation function is employed. The output layer is now given the result of the dot product at the concealed layer. The hidden layer’s output vector and the output layer’s weight matrix are combined to create a dot product in the output layer. The likelihood of words appearing in the context of w(t) at a specific context location is then calculated using the softmax activation function.
Training Autoencoders models
The input and output of feedforward neural networks that use autoencoders are identical. They reduce the input’s dimension before using this representation to recreate the output. The code, also known as the latent-space representation, is an efficient “summary” or “compression” of the input. Encoder, code, and decoder are the three parts of an autoencoder. The input is compressed by the encoder, which also creates a code. The decoder then reconstructs the input exclusively using the code. Autoencoders are mainly dimensionality reduction algorithms which are data-specific, unsupervised and have lossy output.
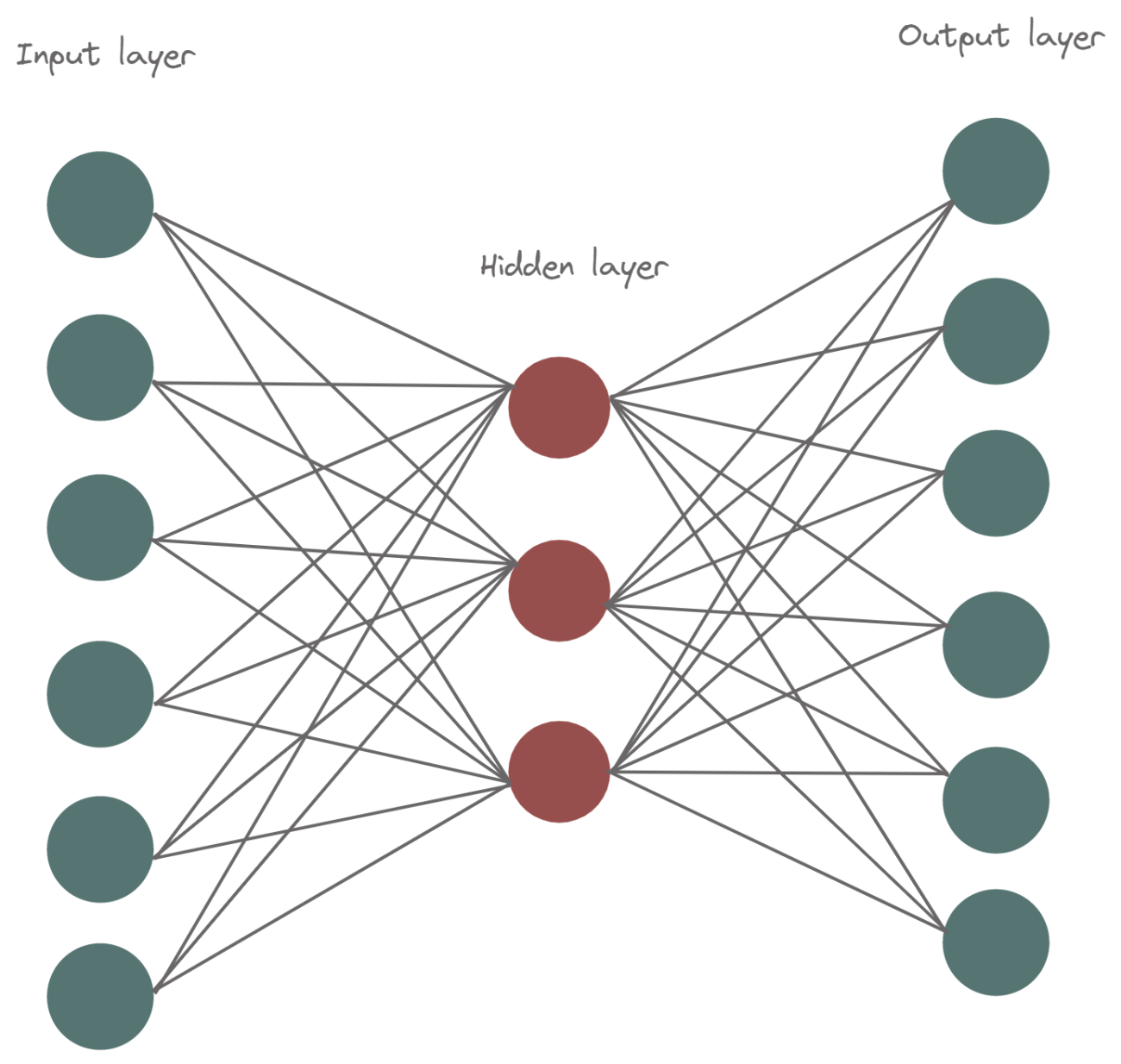
The goal of an autoencoder is to train the network to capture the most crucial elements of the input picture in order to learn a lower-dimensional representation (encoding) for higher-dimensional data, often for dimensionality reduction.
Under the aforementioned generative models, the autoencoder weights are updated via gradient descent, and the revised weights are then normalized in the Euclidean column norm, resulting in a linear convergence to a small neighbourhood of the ground truth. The term “Normalized Gradient Descent” (NGD) refers to a modification of the term “Traditional Gradient Descent” in which each iteration’s updates are only based on the gradients’ directions without regard to their magnitudes. The gradients are normalized to achieve this. Instead of employing the whole set of data, the weight updates are carried out using specific (randomly selected) training examples. By updating the parameters at the conclusion of each mini-batch of samples, mini-batch NGD generalizes.
Training Convolutional Neural Networks
A particular kind of neural network known as a convolutional neural network (CNN) has won several competitions involving computer vision and image processing. A few of CNN’s exciting application areas include speech recognition, object detection, video processing, natural language processing, and image classification and segmentation. The extensive use of feature extraction phases, which may automatically learn representations from data, accounts for Deep CNN’s high learning capacity.
One of CNN’s most enticing properties is its ability to use spatial or temporal correlation in data. Every learning step of CNN is divided into a variety of convolutional layers, nonlinear processing units, and subsampling layers. Using a bank of convolutional kernels, each layer of CNN’s multilayered, feedforward network performs a number of modifications. The convolution process helps to extract useful properties from spatially related data points.
The Convolutional Neural Networks have a forward passway and a backward passway. The forward passway is the subject of the first two sections of the study. The backward passway will be explored in this section. The weighted function will not be verified as to whether it satisfies the request for structure’s accuracy due to the initialization of the weighted function during the CNNs procedure. The function needs to be fixed repeatedly. Backpropagation (BP) is used to propagate correcting errors from upper levels to lower layers. The weighted functions can then be maintained by fixed errors in the lower levels. To locate the fixed errors in CNN, the gradient descent approach is applied.
With the initialization of the procedure, the partial derivative of the loss functions is calculated as a gradient, which measures the trend of the objective function. The accuracy of a function is often measured as the difference between a mathematical model’s output and a sample. The weighted functions in the model are pleased with the request of the process when the difference is less than or equal to the recursion terminal distance. Then, the procedure may end. The learning rate, also known as the step size, determines how much of the gradient is utilized to update the new data. The objective function can ultimately be optimized if it is a convex function.
Conclusion
The gradient descent algorithm finds the global minima of the cost function, for utilizing the optimization method the algorithm must have a cost function. Since the clustering algorithms like hierarchical clustering, agglomerative clustering, etc do not have a cost function the descent method can’t be applied to them. With this article, we have understood the utilization of gradient descent in unsupervised learning.