Bidding optimisation is considered among toughest critical problems in online advertising. Bidding strategies adopt different search pattern, for example, Sponsored Search (SS) which depends on the randomness of the user’s behaviour and the nature of the platform. Display advertising is considered as one of the simple techniques for auction and has taken over Real-Time Bidding resulting in a better performance for the advertisers. In this article, we will explore how Deep Learning techniques are implemented to optimise the Sponsored Search Real Time Bidding (SS-RTB) system in a stochastic environment.
How Does It Work?
A Reinforcement Learning solution for handling the stochastic environment is proposed in the paper titled Deep Reinforcement Learning For Sponsored Search Real Time Bidding by Alibaba group, where the state transition probability is considered for every two days. A robust Markov Decision Process (MDP) model generates data per hour of the impressions performed during the real-time bidding. This model also handles the multi-agent problem. The SS-RTB system is deployed in the e-commerce platform of Alibaba to gather the search pattern and generate the hourly bidding prices.
In Reinforcement Learning, a control system is built on the MDP. This can be mathematically represented by the formula <S, A, p, r>, where S represents the current state, A is the optimal action for that particular state, p denotes the probability function and r is the expected reward for the action A. The transition probability from the state S to S’ taking an action A is denoted by p(s,a,s’) where s, s’ ∈ S. The goal of an MDP model is to learn the optimal policy to maximise the expected long term reward. Applying a technique to an ever-changing environment and implementing deep neural network with reinforcement learning algorithms have resulted in robust models.
Bidding Optimisation
In sponsored search (SS) auctions, bidding strategies have been well developed. However, most of work has been focused on the keyword level auction area, which is concerned with bid price generation for advanced match.
For SS-RTB, the key is to find the optimal_bid price rather than bid_price for the matched keyword pairs during real-time auction, so as to boost an ad’s overall profit. Since the research is to carry out on an e-commerce search auction for Alibaba, in the following example we will use concepts related to the e-commerce search scenario. The goal of the MDP is to find the ad’s maximum purchase amount in a day while simultaneously minimising the cost as well the expenditure. A key point to remember is that the purchase amount should not be less than the ad’s cost.
Dataset
Numerous ads were selected from Alibaba platform, which would cover at least a 100 million auctions per day. The offline dataset was extracted in December and the online dataset was extracted in the next month. Every sample consisted of the clicks, bids and the ranking board. For training, we used the first day’s data, and for validation and testing the next day’s data. A simulator is used to make use of the test data indirectly because the auctions have been already made.
Methodology
The solution has been built on the patterns observed in the real world. It has been found that two consecutive days share the similar patterns in auction sequences in the dynamic environment.
The data has been gathered at the hour as well as second level, for two days — 28-29 January 2018. From the graphs below, it can be seen that the second-level patterns do not match the same type of user behaviour on both the days; whereas the minute and the hourly-level ones showcase a similar pattern. We can infer from the graph that the hourly level data is identical compared to minute level data. Hence, the hourly level data has been considered to formulate the MDP model.
Markov’s Decision Process (MDP)
MDP has the ability to compute the utility of the actions without a model for the environment. It takes the help of action-value pair and the expected reward from the current action. During this process the agent learns to move around the environment and understand the current state which is the optimal policy by taking the action with the highest reward
State Transition:
The number of states are 24 (hours) grouped according to the timestamps. Every group has a set of auctions corresponding to the period. Each state is denoted by <b, t, g’>, where b is the budget, t is the time period and g’ is the feature vector.
Action Space:
The model is controlled by the scheme, where a linear approximator is deployed as the RTB model to aim and fit the optimal_bidprice. The Reinforcement Learning method to find the optimal policy is considered with RTB which gives rise to a development of the linear approximator than the bid.
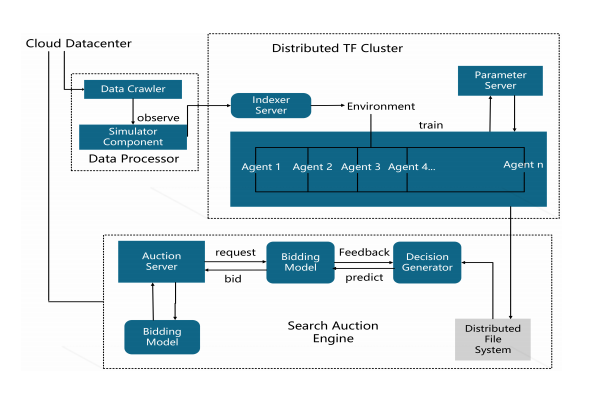
System Architecture
Data Processor:
The RL exploration is handled by the simulator which is the main element. In real world auctions, it is very hard to find the accurate data. The upperhand of the use of simulator is the auctions with unique bids which can be simulated with the help of the entire auction database.
Distributed TensorFlow Cluster:
The RL model is trained on the tensorflow cluster in a varied manner with the servers to facilitate the handling of the weights in the layers. The model was ran on a number of CPUs and GPUs to parallely input the billions of samples since agents have to be trained simultaneously.
Search Auction Engine:
The auction engine is the master component. It sends requests and impression-level features to the bidding model and get bid prices back in real-time.
It has been observed from the iterations that the error is very high at the beginning, but eventually goes down through the process. From this we can infer that the DQN algorithm finds the optimal policy for the state-action pair. A decay has been used to eventually set the randomness of the environment to 0. The hyper-parameter tuning can be done to obtain the optimal policy. After 150 million samples the error seems to decrease to a very low value. This shows that the data required to find the optimal policy is very large.