Along with a large number of applications across the domains, the recommendation systems are increasingly challenged with the issue of huge data and sparsity. It raises concerns about computing costs as well as the inadequate quality of the recommendations. To address this issue, dimensionality reduction techniques are employed in recommendation systems to minimize processing costs and enhance prediction. In this post, we will discuss the collaborative filtering approach of recommendation along with its limitations. We will also try to understand the problem of sparsity faced in this approach and how it can be addressed with dimensionality reduction techniques. We will cover the following major points in this article to understand this concept in detail.
Table of Contents
- Collaborative Filtering
- The Approach to Collaborative Filtering
- Limitation of Collaborative Filtering
- Dimensionality Reduction in Collaborative Filtering
- Singular Value Decomposition
- Principal Component Analysis
Let’s start with understanding collaborative filtering.
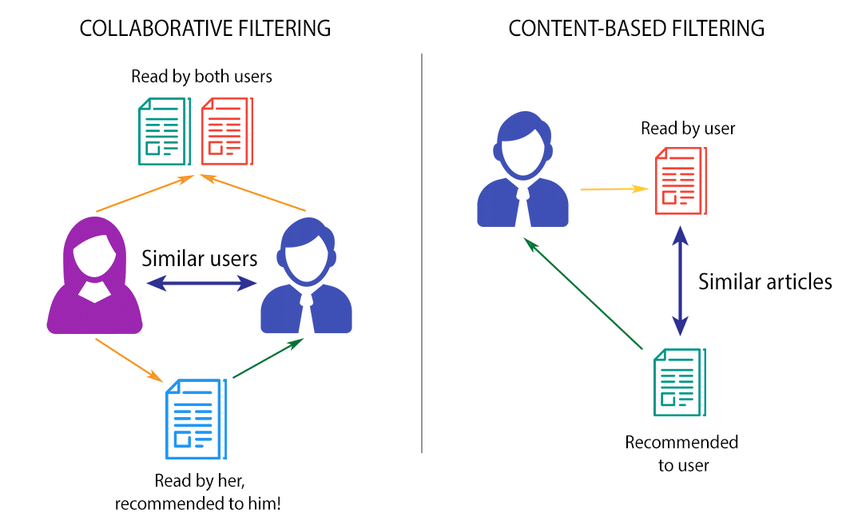
Collaborative Filtering
Collaborative filtering is a famous technique used in most recommendation systems. Generally, collaborative filtering is categorized into two senses: the narrow one and the more general one. Collaborative filtering, in a narrower sense, is a method of creating automatic predictions (filtering) about a user’s interests by gathering preferences or taste information from a large number of users (collaborating).
The collaborative filtering strategy is based on the concept that if person A and person B have the same opinion on a topic, A is more likely to have B’s perspective on a different topic than a randomly selected person. For example, given a partial list of a user’s tastes, a collaborative filtering recommendation system for electronics accessories purchases preferences could offer predictions about which accessories show the user would like to purchase (likes or dislikes). On other hand, in a more general sense, it is the process of searching for information or patterns using strategies that involve several agents, viewpoints, data sources, and so on.
Collaborative filtering applications are generally used with very big data sets. Collaborative filtering methods have been applied to many different types of data, including sensing and monitoring data, such as in mineral exploration, environmental sensing over large areas or multiple sensors; financial data, such as financial service institutions that integrate many financial sources; and electronic commerce and web applications where the focus is on user data, among others.
Approaches to Collaborative Filtering
The majority of collaborative filtering-based recommender systems create a community of like-minded clients. As a measure of closeness, the neighbourhood creation method often uses Pearson correlation or cosine similarity. These algorithms generate two sorts of recommendations after determining the nearby neighbourhood those are,
- Approximation of how much a client C will enjoy a product P. In the case of a correlation-based algorithm, the prediction on product ‘P’ for customer ‘C’ is derived by computing a weighted total of co-rated goods between C and all of his neighbours and then adding C’s average rating to that. This may be represented using the formula below. The prediction is tailored to consumer C.
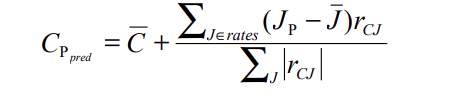
In the above expression, rCJ denotes the correlation between user C and neighbour J and JP is the J’s rating on the product P.
- Recommendation of a product list to a client C. This is sometimes referred to as a top-N suggestion. After forming a neighbourhood, the recommender system algorithm concentrates on the items evaluated by neighbours and selects a list of N products that the client will like.
Limitations of Collaborative Filtering
These systems have been effective in a variety of fields, however, it does not always successfully match things to a user’s preferences. Unless the platform achieves exceptionally high levels of diversity and independence of opinion, one point of view will always predominate over another in a given group. Based on such situations the algorithm has been claimed to have certain flaws, those are:
Sparsity
Because nearest neighbour algorithms rely on exact matches, they sacrifice recommender system coverage and accuracy. Because the correlation coefficient only applies to consumers who have evaluated at least two products in common, many pairings of customers have no correlation at all.
Many commercial recommender systems are used in practice to analyze vast product sets (for example, Amazon.com suggests books). Even active customers may have rated far under 1% of the products in these systems (1% of 2 million volumes is 20,000 books—a vast set on which to form an opinion). As a result, Pearson’s nearest neighbour algorithms may be unable to offer numerous product recommendations for a single consumer. This is known as reduced coverage, and it is caused by sparse neighbour ratings. Furthermore, because only a limited amount of rating data can be provided, the accuracy of suggestions may be poor.
Scalability
Nearest neighbour methods imply computation that rises in parallel with the number of consumers and items. A conventional web-based recommender system employing existing algorithms will have major scalability issues with millions of clients and products.
Synonymy
In the real world, several product names can relate to the same thing. Correlation-based recommender systems are unable to detect this hidden relationship and handle these products differently as a result. Consider two customers who each score ten different recycled letter-pad items as “high,” and another customer who rates ten different recycled memo pad products as “high.”
Correlation-based recommender systems would not be able to compute correlation because there would be no match between product sets, and they would be unable to find the latent relationship that they both like recycled office supplies.
Dimensionality Reduction in Collaborative Filtering
In general, dimensionality reduction is the process of mapping a high-dimensional input space into a reduced level of latent space. Matrix factorization is a subset of dimensionality reduction in which a data matrix D is reduced to the product of many low-rank matrices.
Singular Value Decomposition (SVD)
SVD is a powerful dimensionality reduction technique that is a specialization of the MF approach. The primary issue in an SVD is to discover a reduced dimensional feature space. As SVD is a matrix factorization technique, a m x n matrix R is factored into three matrices as follows:
R = U ⋅ S ⋅V ′
Here, S is a diagonal matrix with all singular values of R as diagonal elements, whereas U and V are two orthogonal matrices. All of the entries in matrix S are positive and are kept in descending order of magnitude.
In recommender systems, SVD is used to accomplish two different tasks: First, it’s used to collect latent relationships between consumers and products, allowing us to calculate a customer’s estimated likelihood of purchasing a specific product. Second, it’s used to make a low-dimensional representation of the original customer-product space and then compute the neighbourhood in that space. It’s then used to provide a list of top-N product suggestions for customers.
Principal Component Analysis (PCA)
PCA is a sophisticated dimensionality reduction technique that is a specific application of the MF approach. PCA is a statistical process that employs an orthogonal transformation to turn a set of possibly correlated observations into a set of values that are linearly uncorrelated variables known as Principal Components (PC).
The number of PCs is less than or equal to the initial variable count. This transformation is defined in such a way that the first PC has the most variance feasible and each subsequent component has the greatest variance possible while being orthogonal to the preceding components. Because they are the eigenvectors of the covariance matrix, the principal components are orthogonal. The relative scaling of the original variables affects PCA.
Conclusion
So here in this post, we have seen collaborative filtering, any kind of ML algorithm if exposed to high dimensional data it will return bad predictions, the collaborative filtering also experiences the same thing. To address this issue we first understand the approach of CF and under which circumstances it fails. Based on flaws we have seen how SVD and PCA can be used to address this issue.