Probability is an integral part of Machine Learning algorithms. We use it to predict the outcome of regression or classification problems. We apply what’s known as conditional probability or Bayes Theorem along with Gaussian Distribution to predict the probability of a class or a value, given a condition. The pair is also used in optimising hyperparameters for an ML model and the process is known as Bayesian Optimization.
In this article, we will learn to implement Bayesian Optimization to find optimal parameters for any machine learning model.
Bayesian Optimization Simplified
In one of our previous articles, we learned about Grid Search which is a popular parameter-tuning algorithm that selects the best parameter list from a given set of specified parameters. Considering the fact that we initially have no clue on what value to begin with for the parameters, it can only be as good as or slightly better than random search.
For computationally intensive tasks, grid search and random search can be painfully time-consuming with less luck of finding optimal parameters. These methods hardly rely on any information that the model learned during the previous optimizations. Bayesian Optimization on the other hand constantly learns from previous optimizations to find a best-optimized parameter list and also requires fewer samples to learn or derive the best values.
Two common terms that you will come across when reading any material on Bayesian optimization are :
- Surrogate model and
- Acquisition function.
The Gaussian process is a popular surrogate model for Bayesian Optimization. What it does is that it defines a prior function that can be used to learn from previous predictions or believes about the objective function.
Acquisition function, on the other hand, is responsible for predicting the sampling points in the search space. Acquisition function follows the exploration and exploitation principle. It is a function that allows the optimizer to exploit an optimal region until a better value is obtained. The goal is to maximise the acquisition function to determine the next sampling point. The terms exploration and exploitation might seem familiar to you if you have learned about Thompson Sampling or Upper Confidence Bound which revolves around the same principle. These are also used as acquisition functions.
A Shallow Dive Into The Math Behind It
The Optimization algorithm
The Acquisition Function
For a deeper understanding of the math behind Bayesian Optimization check out this link.
Implementing Bayesian Optimization For XGBoost
Without further ado let’s perform a Hyperparameter tuning on XGBClassifier.
Given below is the parameter list of XGBClassifier with default values from it’s official documentation:
(max_depth=3, learning_rate=0.1, n_estimators=100, verbosity=1, silent=None, objective=’binary:logistic’, booster=’gbtree’, n_jobs=1, nthread=None, gamma=0, min_child_weight=1, max_delta_step=0, subsample=1, colsample_bytree=1, colsample_bylevel=1, colsample_bynode=1, reg_alpha=0, reg_lambda=1, scale_pos_weight=1, base_score=0.5, random_state=0, seed=None, missing=None)
We will try to find optimal values for max_depth, learning_rate, n_estimators and gamma using Bayesian optimization and we will compare the effects on a model built with default parameters.
Installing Bayesian Optimization
On the terminal type and execute the following command :
pip install bayesian-optimization
If you are using the Anaconda distribution use the following command:
conda install -c conda-forge bayesian-optimization
For official documentation of the bayesian-optimization library, click here.
Dataset: Here we will use XGBClassifier on a preprocessed subset of the training dataset from MachineHack’s Whose Line Is It Anyway: Identify The Author Hackathon.
First, we will use XGBClassifier with default parameters to later compare it with the result of tuned parameters.
XGBClassifier with Default Parameters
#Initializing an XGBClassifier with default parameters and fitting the training data
from xgboost import XGBClassifier
classifier1 = XGBClassifier().fit(text_tfidf, clean_data_train['author'])
- In the above code block, text_tfidf is the TF_IDF transformed texts of the training dataset.
#Predicting for training set
train_p1 = classifier1.predict(text_tfidf)
#Printing the classification report
from sklearn.metrics import classification_report, confusion_matrix
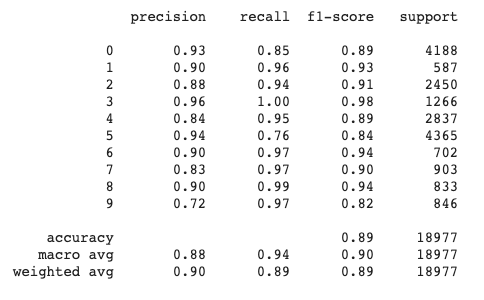
print(classification_report(train_p1, clean_data_train['author']))
Output:
#Accuracy obtained on the training set
cm = confusion_matrix(train_p1, clean_data_train['author'])
acc = cm.diagonal().sum()/cm.sum()
print(acc)
Output:
0.8910786741845392
XGBClassifier With Tuned Parameters
#Importing necessary libraries
from bayes_opt import BayesianOptimization
import xgboost as xgb
from sklearn.metrics import mean_squared_error
#Converting the dataframe into XGBoost’s Dmatrix object
dtrain = xgb.DMatrix(text_tfidf, label=clean_data_val['author'])
#Bayesian Optimization function for xgboost
#specify the parameters you want to tune as keyword arguments
def bo_tune_xgb(max_depth, gamma, n_estimators ,learning_rate):
params = {'max_depth': int(max_depth),
'gamma': gamma,
'n_estimators': int(n_estimators),
'learning_rate':learning_rate,
'subsample': 0.8,
'eta': 0.1,
'eval_metric': 'rmse'}
#Cross validating with the specified parameters in 5 folds and 70 iterations
cv_result = xgb.cv(params, dtrain, num_boost_round=70, nfold=5)
#Return the negative RMSE
return -1.0 * cv_result['test-rmse-mean'].iloc[-1]
#Invoking the Bayesian Optimizer with the specified parameters to tune
xgb_bo = BayesianOptimization(bo_tune_xgb, {'max_depth': (3, 10),
'gamma': (0, 1),
'learning_rate':(0,1),
'n_estimators':(100,120)
})
#performing Bayesian optimization for 5 iterations with 8 steps of random exploration with an #acquisition function of expected improvement
xgb_bo.maximize(n_iter=5, init_points=8, acq='ei')
Output:
Note:
The the process iterates for 8(init_points) + 5(n_iter) = 13 times
#Extracting the best parameters
params = xgb_bo.max['params']
print(params)
#Converting the max_depth and n_estimator values from float to int
params['max_depth']= int(params['max_depth'])
params['n_estimators']= int(params['n_estimators'])
#Initialize an XGBClassifier with the tuned parameters and fit the training data
from xgboost import XGBClassifier
classifier2 = XGBClassifier(**params).fit(text_tfidf, clean_data_train['author'])
#predicting for training set
train_p2 = classifier2.predict(text_tfidf)
#Looking at the classification report
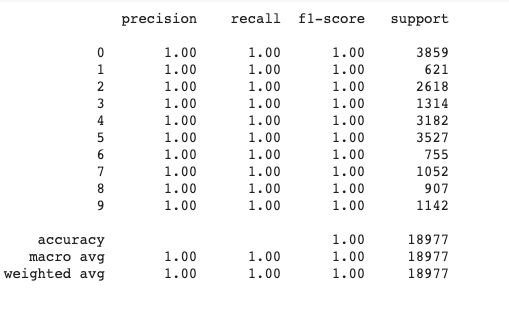
print(classification_report(train_p2, clean_data_train['author']))
Output:
#Attained prediction accuracy on the training set
cm = confusion_matrix(train_p2, clean_data_train['author'])
acc = cm.diagonal().sum()/cm.sum()
print(acc)
Output:
0.9990514833746114
We can see that the prediction for the training set is all exact which even though is practically overfitting, we can see the effect of the optimized parameters on the training set.
The accuracy of prediction with default parameters was around 89% which on tuning the hyperparameters with Bayesian Optimization yielded an impossible accuracy of almost 100%. Bayesian Optimization is a very effective strategy for tuning any ML model.