It is practically impossible to remove noise completely from a dataset which justifies the high usage of probability and statistics in machine learning models. Probability helps to quantify uncertainty caused due to noise in a prediction. Overfitting is a major problem as far as any machine learning algorithm is concerned. And it has been proven that adding noise can regularise and reduce overfitting to a certain level.
With this tutorial, we will take a look at how noise can help achieve better results in ML with the help of the Keras framework. This tutorial has referenced and was inspired by Jason Brownlee’s tutorial on How to Improve Deep Learning Model Robustness by Adding Noise.
Gaussian Noise Layer
The Gaussian Noise Layer in Keras enables us to add noise to models. The layer requires the standard deviation of the noise to be specified as a parameter as given in the example below:
The Gaussian Noise Layer will add noise to the inputs of a given shape and the output will have the same shape with the only modification being the addition of noise to the values.
Ways Of Fitting Noise To A Neural Network
Fitting to input Layer
Between hidden layers in the model
Before the activation function.
After the activation function.
Noise Regularisation
Let us understand the effect of noise on a binary classification problem with the help of a simple example. We will consider a binary classification problem that defines two 2D concentric circles of observations. We will use the sklearn.datasets.make_circles function to generate our sample dataset.
Code:
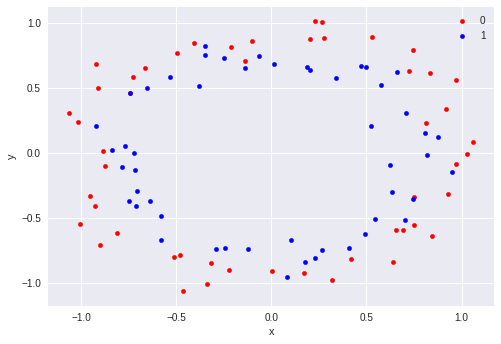
The dataset would look like this:
The dataset consists of 2 independent variables ‘x’ and ‘y’ of the same scale and a dependent variable ‘label’ with values either 0 or 1.
Plotting the dataset:
Code:
Output:
We can see that the data points collectively results in almost 2 circle-like shapes, red and blue with the same centre. Hence the name “circles” dataset.
Now that we have our sample dataset ready, we will create Machine Learning models to analyse the result of noises in a dataset.
Overfitting a Multilayer Perceptron
We will first create a traditional Multilayer Perceptron model. Adding more nodes than what may be required to solve the problem and training the model for a long time can ensure overfitting.
From the 100 samples, we generated We will use 30 observations to train our model and 70 observations to validate or test our model’s performance.
Code:
Output
Train: 1.000, Test: 0.757
Observation
- The model achieved a 75% accuracy on the test set.
- Test accuracy of the overfit model increases to a point and then begins to decrease again.
MLP With Input Layer Noise
On a small dataset inducing noises can have the effect of creating more samples or resampling the domain, making the structure of the input space artificially smother. This will help in making the problem easier to learn and improves generalisation performance.
We will now add a Gaussian Noise layer as the input layer and Gaussian Noise with a mean of 0.0 and a standard deviation 0f 0.01.
Code:
Output
Train: 1.000, Test: 0.771
Observation
- The model achieved a 77% accuracy on the test set.
- The noise causes the accuracy of the model to jump around during training, possibly due to the noise-introducing points that conflict with true points from the training dataset.
- Test accuracy of the model increases to a point and then begins to decrease again showing the presence of overfitting.
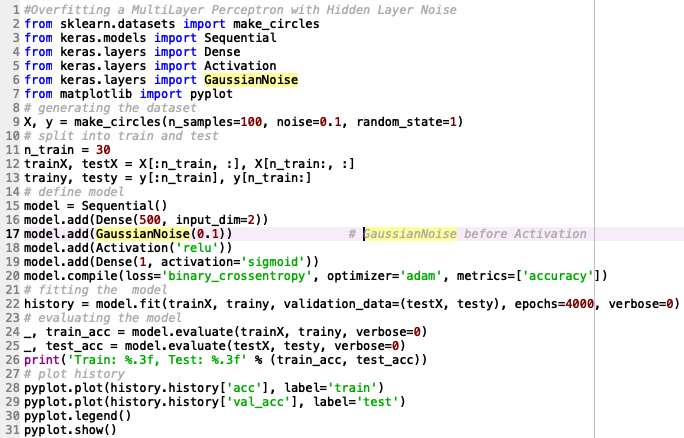
MLP With Hidden Layer Noise
We will now try the alternate approach of adding the Gaussian Noise Layer as the Hidden Layer.
Code:
Output
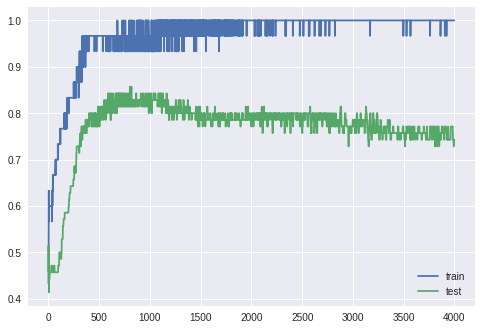
Train: 0.967, Test: 0.814
Observation
- The model achieved an 81% accuracy on the test set.
- The model no longer appears to show the properties of overfitting by keeping an almost constant accuracy after a threshold similar to the behaviour of the training set data.
Note:
- We can also add the noise after the activation function.
- Your values in the results will vary, given both the stochastic nature of the learning algorithm and the stochastic nature of the noise being added to the model