When we talk about Machine Learning or Data Science or any process that involves predictive analysis using data — regression, overfitting and regularization are terms that are often used. Understanding regularization and the methods to regularize can have a big impact on a Predictive Model in producing reliable and low variance predictions.

In this article, we will learn to implement one of the key regularization techniques in Machine Learning using scikit learn and python.

What is Regularization?

Overfitting is one of the most annoying things about a Machine Learning model. After all those time-consuming processes that took to gather the data, clean and preprocess it, the model is still incapable to give out an optimised result.  There can be lots of noises in data which may be the variance in the target variable for the same and exact predictors or irrelevant features or it can be corrupted data points. The ML model is unable to identify the noises and hence uses them as well to train the model. This can have a negative impact on the predictions of the model. This is called overfitting.

In simple words, overfitting is the result of an ML model trying to fit everything that it gets from the data including noises.

Why regularization?

Regularization is intended to tackle the problem of overfitting. Overfitting becomes a clear menace when there is a large dataset with thousands of features and records. Ridge regression and Lasso regression are two popular techniques that make use of regularization for predicting.

Both the techniques work by penalising the magnitude of coefficients of features along with minimizing the error between predictions and actual values or records. The key difference however, between Ridge and Lasso regression is that Lasso Regression has the ability to nullify the impact of an irrelevant feature in the data, meaning that it can reduce the coefficient of a feature to zero thus completely eliminating it and hence is better at reducing the variance when the data consists of many insignificant features. Ridge regression, however, can not reduce the coefficients to absolute zero. Ridge regression performs better when the data consists of features which are sure to be more relevant and useful.

Lasso Regression

Lasso stands for Least Absolute Shrinkage and Selection Operator. Let us have a look at what Lasso regression means mathematically:

Residual Sum of Squares + λ * (Sum of the absolute value of the magnitude of coefficients)

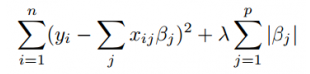
Where,

• λ denotes the amount of shrinkage
• λ = 0 implies all features are considered and it is equivalent to the linear regression where only the residual sum of squares are considered to build a predictive model
• λ = ∞ implies no feature is considered i.e, as λ closes to infinity it eliminates more and more features
• The bias increases with increase in λ
• variance increases with decrease in λ

Implementing Lasso Regression In Python

For this example code, we will consider a dataset from Machinehack’s Predicting Restaurant Food Cost Hackathon.

Consider going through the following article to help you with Data Cleaning and Preprocessing:

A Complete Guide to Cracking The Predicting Restaurant Food Cost Hackathon By MachineHack

After completing all the steps till Feature Scaling(Excluding) we can proceed to building a Lasso regression. We are avoiding feature scaling as the lasso regressor comes with a parameter that allows us to normalise the data while fitting it to the model.

Lets Code!

import numpy as np

Creating a New Train and Validation Datasets

from sklearn.model_selection import train_test_split
data_train, data_val = train_test_split(new_data_train, test_size = 0.2, random_state = 2)

Classifying Predictors and Target

#Classifying Independent and Dependent Features
#_______________________________________________
#Dependent Variable
Y_train = data_train.iloc[:, -1].values
#Independent Variables
X_train = data_train.iloc[:,0 : -1].values
#Independent Variables for Test Set
X_test = data_val.iloc[:,0 : -1].values

Evaluating The Model With RMLSE

def score(y_pred, y_true):
error = np.square(np.log10(y_pred +1) - np.log10(y_true +1)).mean() ** 0.5
score = 1 - error
return score

actual_cost = list(data_val['COST'])
actual_cost = np.asarray(actual_cost)

Building the Lasso Regressor

######################################################################
#Lasso Regression
############################################################################
from sklearn.linear_model import Lasso

#Initializing the Lasso Regressor with Normalization Factor as True
lasso_reg = Lasso(normalize=True)

#Fitting the Training data to the Lasso regressor
lasso_reg.fit(X_train,Y_train)

#Predicting for X_test
y_pred_lass =lasso_reg.predict(X_test)

#Printing the Score with RMLSE
print("\n\nLasso SCORE : ", score(y_pred_lass, actual_cost))

Output:

0.7335508027883148

The Lasso Regression attained an accuracy of 73% with the given Dataset

Also, check out the following resources to help you more with this problem:

1. Guide To Implement StackingCVRegressor In Python With MachineHack’s Predicting Restaurant Food Cost Hackathon
2. Model Selection With K-fold Cross Validation — A Walkthrough with MachineHack’s Food Cost Prediction Hackathon
3. Flight Ticket Price Prediction Hackathon: Use These Resources To Crack Our MachineHack Data Science Challenge
4. Hands-on Tutorial On Data Pre-processing In Python
5. Data Preprocessing With R: Hands-On Tutorial
6. Getting started with Linear regression Models in R
7. How To Create Your first Artificial Neural Network In Python
8. Getting started with Non Linear regression Models in R
9. Beginners Guide To Creating Artificial Neural Networks In R