|
Listen to this story
|
Back in November 2022, when David Smith, a hobbyist who loves playing around with shapes, came across a shape (a tile) that could fill an entire plane without forming regular patterns, he immediately contacted computer scientist Craig Kaplan. Kaplan, who had been in search of such a shape for decades, albeit using a computational approach, began running his software on this shape. By the end of January, they had proof of a wonderful open problem that occupied their minds for a long time.
The Problem
Imagine the tiling to be the same as your bathroom floor tiling where a square grid is repeated multiple times until it fills the entire surface without leaving any gaps. However, mathematicians have long been searching for a shape that can be tiled in a similar way, except it won’t form a pattern, even when extended infinitely. The tile doesn’t have to be a square grid. It can be a parallelogram or just about any shape that prevents the emergence of periodicity.
“There are lots of examples of sets of shapes that tile aperiodically, but it was unknown whether a single shape could do it.” The best people have been able to do is with two shapes, most famously by Penrose tiling, which prohibited periodicity using two different rhombi, or two different quadrilaterals.
Seems like we finally have the answer. Called the ‘hat’ (since it vaguely resembles a fedora), the crinkly kind of shape can be fit together in a number of ways.
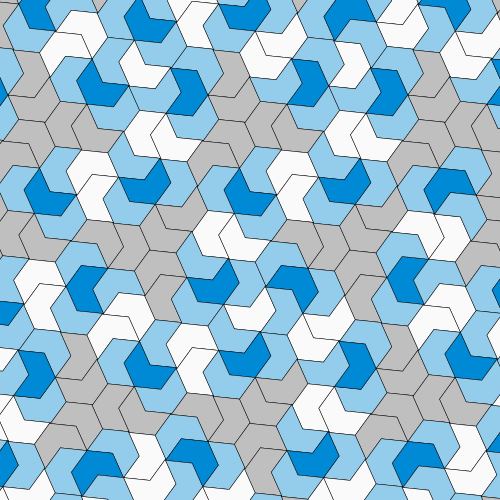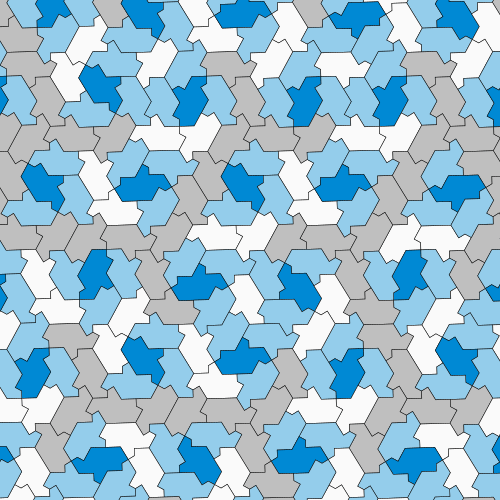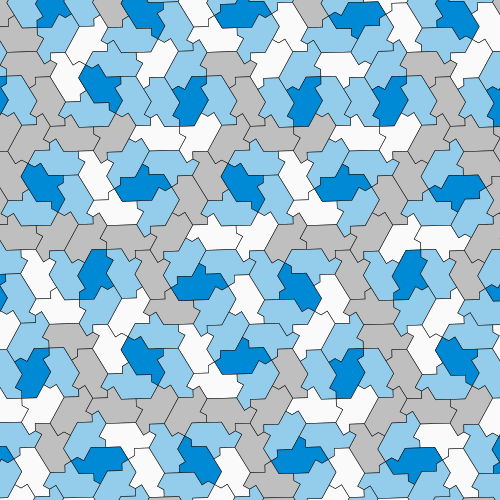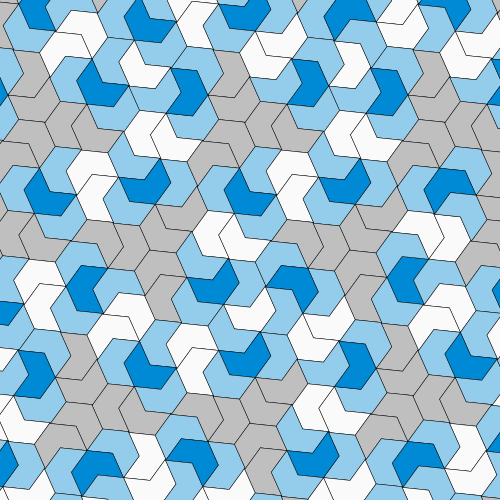
“Like, there’s some number of ways you could put two hats together. And from that, there’s some number of ways that you can maybe put a ring of hats around a single hat, and from that maybe there’s some number of ways you could build two rings of hats and on and on,” said Kaplan. Thus, we are met with a combinatorial explosion of things to be kept track of, which gets incredibly tedious and error prone.
Computation x mathematics
Kaplan had written a software that could take a shape and “build a big block of them by brute force.” This acted as the raw data for researchers to intuitively study and find patterns in the large patch of tiles.
Using computational methods, the researchers tried to analyse the tiling properties of the hat, including its Heesch number (which tells if layers of copies of the shape can surround a central copy without leaving any gaps) and isohedral number (which measures the number of ways the shape can be oriented to create a repeatable pattern). The results were that the shape shattered the record for both Heesch numbers and isohedral numbers by a wide margin – proving itself to be an Einstein.
The term ‘Einstein’, a play on the physicist Albert Einstein, comes from German ein Stein meaning “one stone,” referring to a single tile. It is used to describe the property of the tile to fill an entire plane, without repeating itself in regular intervals.
However, even after using intuition to understand the structure of the tiling, Kaplan mentions that software was important as part of their proof that the produced tiling was aperiodic.
One way to measure a tile doesn’t repeat itself is to look at all possible neighbourhoods that might contain around each tile, which is a finite number. By extension, it also means that there are only finitely possible neighbourhoods that can occur in an infinite tiling. The researchers used computation to construct a complete list of all possible neighbourhoods, and then further computation to verify that all such neighbourhoods have the properties that they need them to have in order to prove aperiodicity.
“At a high level, the computation shows via exhaustive enumeration that we can always group individual tiles into clusters in a unique, forced way, and that we can group clusters into larger clusters, and those into even larger clusters, and so on ad infinitum,” added Kaplan.
This forced hierarchy of clustering (which refers to the way tiles are arranged in local neighbourhoods) is one way that mathematicians can prove aperiodicity. While in principle all of these rules could have been derived by hand, it made much more sense to the researchers to turn this sort of tedious case-based analysis over to software.
But, to show that the proof is valid for an infinite plane, one cannot just write down where every tile is – because that list would be infinitely long. “You need something more indirect, you need kind of an abstract rule that allows you to know that in principle you can go to infinity in every direction.”
Here, an old theorem in the mathematics of tilings allowed the researchers to kind of bootstrap from large and finite up to infinity. “But, it’s not obvious,” says Kaplan. In fact, part of Kaplan’s independent work has been to study shapes that make copies of themselves and get stuck after a while, as opposed to assuming that once you get big enough, you can keep going forever.
Einstein tiles on toilet paper?
Previously, advances in tiling theory have had applications in other sciences like physics, chemistry, and engineering, most famously between Penrose tilings and quasicrystals. Therefore, Kaplan says that while there is no immediate application identified to this tiling, we can expect new and interesting connections conjuring up as more and more researchers fiddle around with it.
Recently, there have also been a couple of people who have incorporated the Einstein tile into different kinds of games, shortly after the release. Take, for example, a twitter handle by name ZenoRogue, who made a really elegant implementation of the hat on his software, known as Hyperrogue. This software which already had kind of like a minesweeper game could adapt to any grid. It only goes to show that the pace of AI right now is remarkable, where demos are built in no time.
Alongside this, Kaplan also mentioned a famous story from the 1990s, where Kimberly-Clark, the parent company of Kleenex, started to print toilet paper with Penrose tiles on it. However, the company that owned the patent to Penrose tiles sued them saying that this is inappropriate.
“I feel the opposite. I would be flattered to see this design appear on toilet paper and I’m putting that out there for the record,” he remarked.
