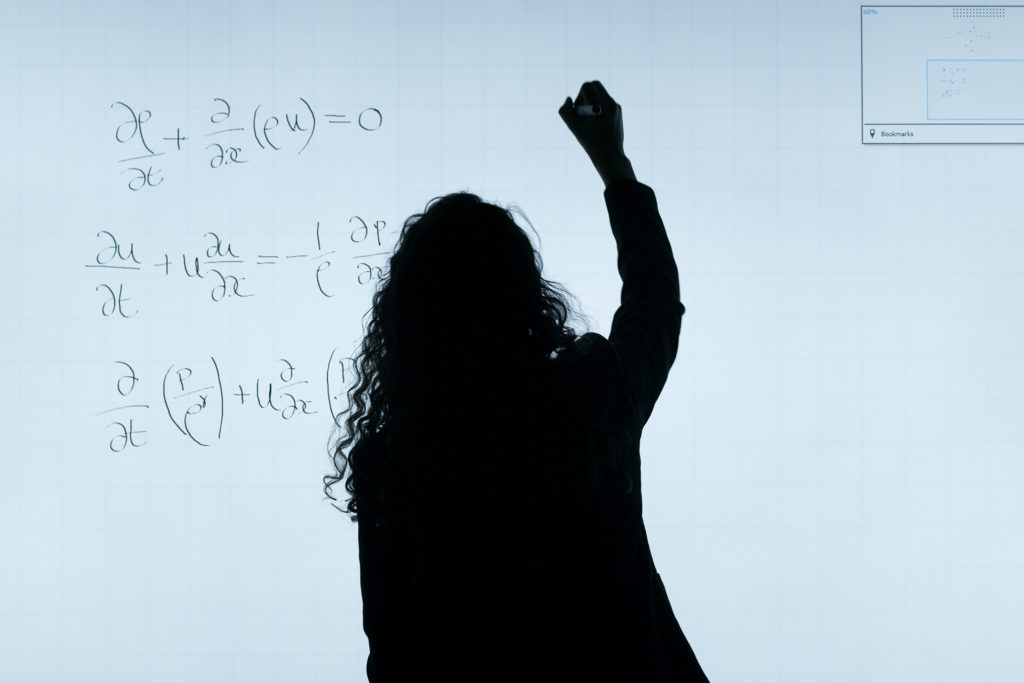Score-based generative models show good performance recently in image generation. In the context of statistics, Score is defined as the gradient of logarithmic probability density with respect to the data distribution parameter. Usually, while training a generative model, noises are added to the original image, and the model learns to revert the noisy image back to its original form. In a score-based generative model, noises are added in steps such that the final noisy image follows a predefined probability distribution. A trained model generates the original image from the predefined distribution following the score estimated at each step during noising.
Yang Song and Stefano Ermon from Stanford University, and Jascha Sohl-Dickstein, Diederik P. Kingma, Abhishek Kumar and Ben Poole from Google Brain have introduced Stochastic Differential Equations (SDE) in a score-based generative model instead of perturbing with noise distributions and denoising in steps. In general, stochastic differential equations are used to transform a complex distribution smoothly and continuously into a predefined simple distribution. Similarly, in this generative model framework, the input image is noised smoothly using a forward SDE. The noisy image follows a predefined distribution. The forward SDE evaluates and learns the score function using neural networks during this transition. A score-based reverse-time SDE can smoothly remove the noises from the predefined distribution and generate the original image.
The major advantage of incorporating an SDE in generative models is that it does not possess any data-dependent trainable parameter and depends purely on the time-dependent score values. Therefore, the generative process by a reverse-time SDE is achieved through a time-dependent neural network that can estimate the score value at any intermediate time mark, originally learned by a forward SDE. This approach can be applied to generative domains, including images, audio, shapes, and graphs.
This framework introduces two SDE solvers while flexibly accepting any SDE solver to integrate with its reverse-time SDE for sampling. The introduced SDE solvers are: Predictor-Corrector sampler that combines a numerical SDE with a score-based model and a probability flow ODE-based deterministic sampler. Since reverse-time SDE can be estimated using unconditional scores, the generation process can be more generalized to any conditional generation without re-training or fine-tuning. Therefore, it solves any inverse problem, including image inpainting, class-conditional generation, and colorization with a single fully-trained SDE model. This unified framework can accept any score-based model into its architecture to produce extraordinary results compared to their original versions. Moreover, this approach generates high-quality and high-fidelity images that no other generative model can generate.
The score-based SDE approach is highly flexible to employ different models and to tune hyperparameters. By varying precision parameters in the Probability flow ODE sampler, the number of score function evaluations (NFE) can be greatly varied. However, the quality of the generated image is uncompromised even at low NFE. Thus, Probability flow ODE sampler yields faster sampling than any other sampling method.
Python Implementation of Score-based SDE
The Score-SDE requires a PyTorch environment and a CUDA GPU runtime. Most of this code implementation references the official notebook of Score-based SDE. Download the source code files from the official repository.
!git clone https://github.com/yang-song/score_sde_pytorch.git
Output:
Change the directory to proceed further with the dependencies and source codes.
%cd score_sde_pytorch/ !ls -p
Output:
Install dependencies and other requirements with pip command as shown below.
# install dependencies !pip install -r requirements.txt
Output:
Download pre-trained model’s checkpoints (around 1 GB) from the official storage as shown below.
!gdown --id 1JInV8bPGy18QiIzZcS1iECGHCuXL6_Nz
Output:
Create a directory exp/ve/cifar10_ncsnpp_continuous/ to move the downloaded checkpoint (further processing expects this path).
# we need this path /content/score_sde_pytorch/exp/ve/cifar10_ncsnpp_continuous %cd /content/score_sde_pytorch/ !mkdir exp/ %cd exp/ !mkdir ve/ %cd ve/ !mkdir cifar10_ncsnpp_continuous/ %cd cifar10_ncsnpp_continuous
Output:
Move the downloaded checkpoint to the newly created directory using the following command.
# move checkpoint to the newly created directory %cd /content/score_sde_pytorch/ !mv checkpoint_24.pth /content/score_sde_pytorch/exp/ve/cifar10_ncsnpp_continuous/
Check the directory for file availability.
%cd /content/score_sde_pytorch/exp/ve/cifar10_ncsnpp_continuous/ !ls
Output:
Create the environment by importing the necessary libraries and modules.
%load_ext autoreload %autoreload 2 from dataclasses import dataclass, field import matplotlib.pyplot as plt import io import csv import numpy as np import pandas as pd import seaborn as sns import matplotlib import importlib import os import functools import itertools import torch from losses import get_optimizer from models.ema import ExponentialMovingAverage import torch.nn as nn import numpy as np import tensorflow as tf import tensorflow_datasets as tfds import tensorflow_gan as tfgan import tqdm import io import likelihood import controllable_generation from utils import restore_checkpoint sns.set(font_scale=2) sns.set(style="whitegrid")
import models from models import utils as mutils from models import ncsnv2 from models import ncsnpp from models import ddpm as ddpm_model from models import layerspp from models import layers from models import normalization import sampling from likelihood import get_likelihood_fn from sde_lib import VESDE, VPSDE, subVPSDE from sampling import (ReverseDiffusionPredictor, LangevinCorrector, EulerMaruyamaPredictor, AncestralSamplingPredictor, NoneCorrector, NonePredictor, AnnealedLangevinDynamics) import datasets
Build the SDE model using the following codes.
%cd /content/score_sde_pytorch/ from configs.ve import cifar10_ncsnpp_continuous as configs ckpt_filename = "exp/ve/cifar10_ncsnpp_continuous/checkpoint_24.pth" config = configs.get_config() sde = VESDE(sigma_min=config.model.sigma_min, sigma_max=config.model.sigma_max, N=config.model.num_scales) sampling_eps = 1e-5
Build a score-based generative model and restore the downloaded checkpoint.
batch_size = 64 config.training.batch_size = batch_size config.eval.batch_size = batch_size random_seed = 0 sigmas = mutils.get_sigmas(config) scaler = datasets.get_data_scaler(config) inverse_scaler = datasets.get_data_inverse_scaler(config) score_model = mutils.create_model(config) optimizer = get_optimizer(config, score_model.parameters()) ema = ExponentialMovingAverage(score_model.parameters(), decay=config.model.ema_rate) state = dict(step=0, optimizer=optimizer, model=score_model, ema=ema) state = restore_checkpoint(ckpt_filename, state, config.device) ema.copy_to(score_model.parameters())
Define helper functions to display images for the proceeding generative examples.
def image_grid(x): size = config.data.image_size channels = config.data.num_channels img = x.reshape(-1, size, size, channels) w = int(np.sqrt(img.shape[0])) img = img.reshape((w, w, size, size, channels)).transpose((0, 2, 1, 3, 4)).reshape((w * size, w * size, channels)) return img
def show_samples(x):
x = x.permute(0, 2, 3, 1).detach().cpu().numpy()
img = image_grid(x)
plt.figure(figsize=(8,8))
plt.axis('off')
plt.imshow(img)
plt.show()
Develop a Predictor (ReverseDiffusionPredictor) and a Corrector (LangevinCorrector) to perform Predictor-Corrector (PC) sampling.
img_size = config.data.image_size channels = config.data.num_channels shape = (batch_size, channels, img_size, img_size) predictor = ReverseDiffusionPredictor corrector = LangevinCorrector snr = 0.16 n_steps = 1 probability_flow = False sampling_fn = sampling.get_pc_sampler(sde, shape, predictor, corrector, inverse_scaler, snr, n_steps=n_steps, probability_flow=probability_flow, continuous=config.training.continuous, eps=sampling_eps, device=config.device) x, n = sampling_fn(score_model) show_samples(x)
Output:
Develop a Probability flow ODE sampler to get likelihood and a unique embedded data representation.
shape = (batch_size, 3, 32, 32) sampling_fn = sampling.get_ode_sampler(sde, shape, inverse_scaler, denoise=True, eps=sampling_eps, device=config.device) x, nfe = sampling_fn(score_model) show_samples(x)
Output:
Compute the Likelihood for each image in the dataset.
train_ds, eval_ds, _ = datasets.get_dataset(config, uniform_dequantization=True, evaluation=True)
eval_iter = iter(eval_ds)
bpds = []
likelihood_fn = likelihood.get_likelihood_fn(sde, inverse_scaler, eps=1e-5)
for batch in eval_iter:
img = batch['image']._numpy()
img = torch.tensor(img).permute(0, 3, 1, 2).to(config.device)
img = scaler(img)
bpd, z, nfe = likelihood_fn(score_model, img)
bpds.extend(bpd)
print(f"average bpd: {torch.tensor(bpds).mean().item()}, NFE: {nfe}")
Output:
Reconstruct the original images using the embedded representations of data.
train_ds, eval_ds, _ = datasets.get_dataset(config, uniform_dequantization=False, evaluation=True)
eval_batch = next(iter(eval_ds))
eval_images = eval_batch['image']._numpy()
shape = (batch_size, 3, 32, 32)
likelihood_fn = likelihood.get_likelihood_fn(sde, inverse_scaler, eps=1e-5)
sampling_fn = sampling.get_ode_sampler(sde, shape, inverse_scaler, denoise=True, eps=sampling_eps, device=config.device)
plt.figure(figsize=(18, 6))
plt.subplot(1, 2, 1)
plt.axis('off')
plt.imshow(image_grid(eval_images))
plt.title('Original images')
eval_images = torch.from_numpy(eval_images).permute(0, 3, 1, 2).to(config.device)
_, latent_z, _ = likelihood_fn(score_model, scaler(eval_images))
x, nfe = sampling_fn(score_model, latent_z)
x = x.permute(0, 2, 3, 1).cpu().numpy()
plt.subplot(1, 2, 2)
plt.axis('off')
plt.imshow(image_grid(x))
plt.title('Reconstructed images')
Output:
We can visualize that the Probability Flow ODE reconstructs images with greater visual quality.
Now, we can use the built model for controlled generations. First, we generate inpainting images. The model will generate the image portions where the original images are masked.
train_ds, eval_ds, _ = datasets.get_dataset(config) eval_iter = iter(eval_ds) bpds = [] predictor = ReverseDiffusionPredictor corrector = LangevinCorrector snr = 0.16 n_steps = 1 probability_flow = False pc_inpainter = controllable_generation.get_pc_inpainter(sde, predictor, corrector, inverse_scaler, snr=snr, n_steps=n_steps, probability_flow=probability_flow, continuous=config.training.continuous, denoise=True) batch = next(eval_iter) img = batch['image']._numpy() img = torch.from_numpy(img).permute(0, 3, 1, 2).to(config.device) show_samples(img) mask = torch.ones_like(img) mask[:, :, :, 16:] = 0. show_samples(img * mask) x = pc_inpainter(score_model, scaler(img), mask) show_samples(x)
Output:
It is observed that most of the masked images were inpainted correctly to their original version. Secondly, we apply the built model for colourization tasks. The model can generate coloured images from grayscale images.
train_ds, eval_ds, _ = datasets.get_dataset(config) eval_iter = iter(eval_ds) bpds = [] predictor = ReverseDiffusionPredictor corrector = LangevinCorrector snr = 0.16 n_steps = 1 probability_flow = False batch = next(eval_iter) img = batch['image']._numpy() img = torch.from_numpy(img).permute(0, 3, 1, 2).to(config.device) show_samples(img) gray_scale_img = torch.mean(img, dim=1, keepdims=True).repeat(1, 3, 1, 1) show_samples(gray_scale_img) gray_scale_img = scaler(gray_scale_img) pc_colorizer = controllable_generation.get_pc_colorizer( sde, predictor, corrector, inverse_scaler, snr=snr, n_steps=n_steps, probability_flow=probability_flow, continuous=config.training.continuous, denoise=True ) x = pc_colorizer(score_model, gray_scale_img) show_samples(x)
Output:
It is observed that most colours are restored back to their original, while very few colours are different from the original.
Wrapping Up Score-based SDE
Score-based Stochastic Differential Equations is a generalized framework meant exclusively for image generation. With a PC sampler and a Probability flow ODE sampler, Score-based SDE models yield both faster and more accurate outputs than existing approaches. This approach achieves an extraordinary Inception Score of 9.89 and an FID of 2.2 for unconditional image generation on CIFAR-10 image dataset. Thus, the Score-based SDE approach is presently the state-of-the-art in generative modeling tasks, including class-conditioned image generation, image inpainting, image colourization, high-fidelity high-resolution image generation.