Convolutional Neural Networks have the limitation that they learn inefficiently if the data or model dimension is very large. So, Seunghyeok Oh et al. showed how to make use of quantum computation and CNN to develop a more efficient and outperforming technique that can be applied to solve complex machine learning tasks. This technique which integrates both CNN and quantum computing is referred to as Quantum Convolutional Neural Network (QCNN). In this post, we will have an in-depth understanding of QCNN with its paradigm and applications. The following are the key points to be discussed in this article.
Table of Contents
- The Standard CNN
- What is Quantum Computing?
- The Paradigm of QuantumCNN (QCNN)
- Applications of QCNN
Let’s start the discussion by taking revision of how the CNN addresses the tasks.
The Standard CNN
Among many classification models, the Convolutional Neural Network (CNN) has demonstrated exceptional performance in computer vision. Photographs and other images that reflect the real world have a high correlation between surrounding pixels.
The fully-connected layer, which is a fundamental model in deep learning, performed well in machine learning, but there is no way to maintain the correlation. CNN, on the other hand, can directly store correlation information, resulting in a more accurate performance evaluation.
CNN works primarily by stacking the convolution and pooling layers. The convolution layer uses linear combinations between surrounding pixels to find new hidden data. The pooling layer shrinks the feature map, lowering the learning resources required and preventing overfitting.
The classification result is obtained using the fully connected layer after the data size has been reduced sufficiently by repeatedly applying these layers. For better results, the loss between the acquired label and the actual label can be used to train the model using a gradient descent method or other optimizers.
Many studies have been published that combine the quantum computing system and the CNN model is capable of solving the problems of the real world which are difficult with machine learning using the Quantum Convolutional Neural Network (QCNN).
There is a method for solving quantum physics problems efficiently by applying the CNN structure to a quantum system, as well as a method for improving performance by adding a quantum system to problems previously solved by CNN.
Before proceeding to the QCNN, we first need to understand what is Quantum computing and computation.
What is Quantum Computing?
Quantum computing is gaining traction as a new way to solve problems that traditional computing techniques can’t solve. Quantum computers have a different computing environment than traditional computers.
Quantum computers, in particular, can use superposition and entanglement, which are not seen in traditional computing environments, to achieve high performance through qubit parallelism. Here qubit is referred to as the quantum bit which is basically a unit of quantum information.
Quantum computing is seen as a new solution to algorithmic problems that are difficult to solve because of these advantages. Various studies using quantum computing models are also being conducted in the field of machine learning. Furthermore, since the optimization of quantum devices using the gradient descent method has been studied, It is possible to learn quantum machine learning using hyperparameters quickly.
The Paradigm of QuantumCNN
QCNN, or Quantum Convolutional Neural Network extends the key features and structures of existing CNN to quantum systems. When a quantum physics problem defined in the many-body Hilbert space is transferred to a classical computing environment, the data size grows exponentially in proportion to the system size, making it unsuitable for efficient solutions. Because data in a quantum environment can be expressed using qubits, the problem can be avoided by applying a CNN structure to a quantum computer.
Now, let us have a look at the architecture of the QCNN model.
As shown in the above architecture, the QCNN model applies the convolution layer and the pooling layer which are the key features of CNN, to the quantum systems.
- The hidden state is discovered by applying multiple qubit gates between adjacent qubits in the convolution circuit.
- The pooling circuit reduces the quantum’s system size by observing the qubit fraction or applying CNOT gates to nothing but two-qubit gates.
- Re-create the convolution and pooling circuits from steps 1 and 2.
- If the size of the system is small enough, The classification result is predicted by a fully connected circuit.
The Multiscale Entanglement Renormalization Ansatz (MERA) is commonly used to satisfy this structure. MERA is a model for efficiently simulating many-body state quantum systems. MERA now adds qubits to the quantum system, increasing its size exponentially for each depth.
This MERA is used in the opposite direction by QCNN. The reversed MERA, which is suitable as a model of QCNN, reduces the size of the quantum system exponentially from the given data.
Applications of QCNN
One of the most popular applications of CNN is in the field of image classification. In terms of superposition and parallel computation, quantum computers offer significant advantages. Quantum Convolutional Neural Network improves CNN performance by incorporating quantum environments. In this section, we’ll look at how the QCNN can help with image classification.
The quantum convolution layer is a layer in a quantum system that behaves like a convolution layer. To obtain feature maps composed of new data, the quantum convolution layer applies a filter to the input feature map. Unlike the convolution layer, the quantum convolution layer uses a quantum computing environment for filtering.
Quantum computers offer superposition and parallel computation, which are not available in classical computing and can reduce learning and evaluation time. Existing quantum computers, on the other hand, are still limited to small quantum systems.
Small quantum computers can construct the quantum convolution layer because it does not apply the entire image map to a quantum system at once but rather processes it as much as the filter size at a time.
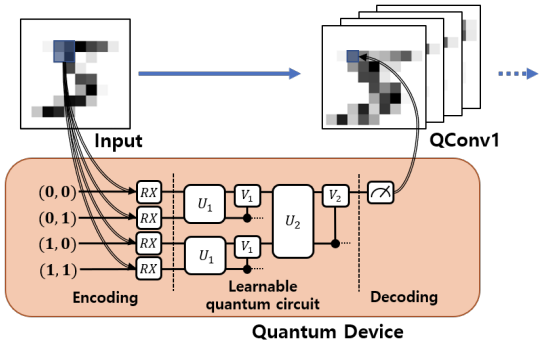
The quantum convolution layer can be constructed as shown in the diagram below. The following is an explanation of how the concept works:
- During the encoding process, the pixel data corresponding to the filter size is stored in qubits.
- Filters in learnable quantum circuits can detect the hidden state from the input state.
- The decoding process obtains new classical data by measuring.
- To finish the new feature map, repeat steps 1–3 once more.
The first step’s encoding is a process that converts classical information into quantum information. The simplest method is to apply a rotation gate to qubits that correspond to pixel data. Of course, different encoding methods exist, and the encoding method chosen can affect the number of qubits required as well as the learning efficiency. The third decoding process is based on the measurement of one or more quantum states. Classical data is determined by measuring quantum states.
A combination of multiple gates can be used to create the random quantum circuit in the second step. By adding variable gates, the circuit can also perform optimization using the gradient descent method. This circuit can be designed in a variety of ways, each of which has an impact on learning performance.
Final Words
Through this article, we have seen how QCNN uses a CNN model and a quantum computing environment to enable a variety of approaches in the field. Fully parameterized quantum convolutional neural networks open up promising results for quantum machine learning and data science applications. Apart from this discussion, if you want to look at a practical implementation of the QCNN, I recommend that you look at the TensorFlow implementation and the researcher’s team as mentioned in the introduction.