One of the most difficult challenges that every precautionary face is the complexity involved in developing algorithms that perform well on training and might well on new inputs. Machine learning employs a variety of techniques to reduce or eliminate test errors. One such technique is regularization. We will discuss why using regularization techniques in the context of regularization is necessary, and we will conclude with a practical demonstration of implementing an activity regularization for the neural network. The following are the key points to be discussed in this article.
Table Of Contents
- Need for Regularization
- What is Regularization?
- Keras Regularizers
- Kernel Regularizer
- Bias Regularizer
- Activity Regularizer
- Implementing the Regularization in a Neural Network
Let’s start the discussion by understanding the need for regularization.
Need for Regularization
Deep neural networks are sophisticated learning models that are prone to overfitting because of their ability to memorize individual training set patterns rather than applying a generalized approach to unrecognizable data. That is why the regularization of neural networks is so important. It aids the neural network’s ability to generalize data that it does not recognize by keeping the learning model simple.
Let’s look at an example to show what we’re talking about. Let’s pretend we have a dataset with both input and output values. Assume there is a true relationship between these values. The goal of deep learning is to approximate the relationship between input and output values as closely as possible. As a result, for each data set, there are two models that can assist us in defining this relationship: a simple model and a complex model.

A straight line exists in the simple model that only includes two parameters that define the relationship in question. A graphical representation of this model will include a straight line that closely passes through the centre of the data set in question, ensuring that the line and the points below and above it have very little distance between them.
The complex model, on the other hand, has several parameters that vary depending on the data set. It uses the polynomial equation to pass through all of the training data points. The training error will eventually reach zero, and the model will memorize the individual patterns in the data set as the data set becomes more complex. Unlike simple models, which aren’t too dissimilar even when trained on different data sets, complex models can’t be said to be the same.
What is Regularization?
A major issue in machine learning is developing algorithms that perform effectively not only on training data but also on new inputs. Many machine learning algorithms are intentionally designed to minimize test error, possibly at the expense of greater training error. These procedures are typically referred to as regularization. Deep learning practitioners can choose from a variety of regularization methods. In fact, one of the key research efforts in the field has been the development of more effective regularization procedures.
Regularizing estimators are used in the majority of deep learning regularization strategies. The regularization of an estimator works by exchanging higher bias for lower variance. An effective regularizer reduces variance while not increasing bias excessively, resulting in a profitable trade.
When we discuss the generalization and overfitting in the model family being trained we encountered three scenarios either (1) excluded the true data-generating process, resulting in underfitting and bias, (2) matched the true data-generating process, or (3) included the generating process but also many other possible generating processes, resulting in an overfitting regime in which variance rather than bias dominates the estimation error.
The goal of regularization is to transfer a model from the third to the second regime.
Keras Regularizers
The weights become more specialized to the training data as we train the model for a longer period of time, resulting in overfitting the training data. The weights will grow in size to handle the specifics of the examples seen in the training data.
When the weights are too heavy, the network becomes unstable. Regardless of whether the weight is tailored to the training dataset, minor variations or statistical noise in the expected inputs will result in significant differences in the output.
In this case, we can use weight regularization to update the learning algorithm and encourage the network to keep the weights small, and it can be used as a general technique to reduce overfitting. Regularizers allow you to apply weight penalties during optimization. These penalties are added together to form the loss function that the network optimizes.
With the help of Keras Functional API, we can facilitate this regularizer in our model layers (e.g. Dense, Conv1D, Conv2D, and Conv3D) directly. These layers expose three-argument or types of regularizers to use, I,e Kernel regularizers, Bias Regulerizers, and Activity Regulerizers which aim to;
- Kernel regularizer penalizes the layer’s kernel(weight) but does not penalize bias.
- Only the bias of the layer is penalized by a bias regularizer.
- The activity regularizer penalizes the output of the layer.
Activity Regularization
Let us understand the activity regularization before jumping to the implementations.
The activity regularization technique is used to encourage a neural network to learn sparse feature representations or we can say internal feature representation of our data that is being fed. Apart from this, this approach is mostly known for reducing the overfitting and to improve the model’s generalization ability to unseen data. Under the hood of this technique, it applies penalties by observing the generalization ability on the validation set.
Implementing the Regularization in a Neural Network
The below code snippets show how we can use these in the layers mentioned above.
from tensorflow.keras.layers import Dense
from tensorflow.keras import regularizers
layer = Dense(500, activation='relu',
kernel_regularizer=regularizers.l1(l1=0.001),
bias_regularizer = regularizers.l2(l2=0.001),
activity_regularizer = regularizers.l1(l1=0.002))
Now we are going to see how activity regularizer can play a significant role when we want to balance both accuracies.
Here we will see how the custom neural network performs on a given set of data, in this case, we will observe the training and validation accuracy of the network before and after the training activity regularizer.
from sklearn.datasets import load_iris from tensorflow.keras.models import Sequential from tensorflow.keras.utils import to_categorical from tensorflow.keras.layers import Dense from sklearn.preprocessing import StandardScaler from sklearn.model_selection import train_test_split
Load and ready the data
iris = load_iris() X = iris.data y = iris.target y = to_categorical(y) ss = StandardScaler() X = ss.fit_transform(X) X_train, X_test, y_train, y_test = train_test_split(X,y)
Now below we build the 5 layers artificial neural network, and first, we train it will observe the accuracies.
model_1 = Sequential([
Dense(512, activation='tanh', input_shape = X_train[0].shape),
Dense(512//2, activation='tanh'),
Dense(512//8, activation='tanh'),
Dense(32, activation='relu'),
Dense(3, activation='softmax')
])
print(model1.summary())
model_1.compile(optimizer='sgd',loss='categorical_crossentropy', metrics=['acc'])
hist_1 = model_1.fit(X_train, y_train, epochs=350, batch_size=128, validation_data=(X_test,y_test))
The accuracies at the end of 350 epochs 96.43, 92.11 training and validation respectively.
Let’s now try to explore by only applying an activity regularizer. This can be done by setting argument activitity_regularizer by using l1 or l2 norms regularizer.
The L1 and L2 have stated as The L1 norm allows some weights to be large while driving others to zero. It penalizes the true value of a weight. The L2 norm causes all weights to decrease in size. It penalizes the square value of a weight.
Dense(512, activation='tanh', input_shape = X_train[0].shape, activity_regularizer=regularizers.l1(l1=0.001))
Above is the first layer of the same model which we have seen above. The only change is that we have initiated the activity regularizer. And after the model for 350 epochs, we are getting accuracies of 98.21 and 94.74 for training and validation respectively.
The difference that we are getting before and after regularization is nearly +2% which tells us that by applying regularization we can further improve our network performance.
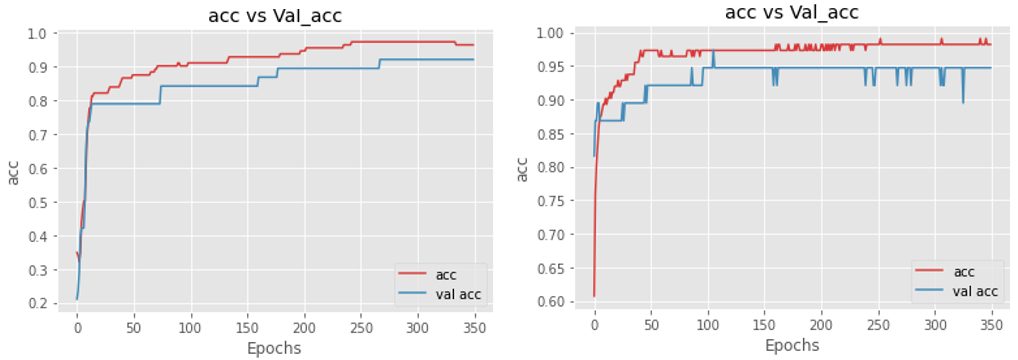
Now let’s see the plots of accuracies for both before and after applying regularization
Conclusion
From the above plot, it is clear that the activity regularizer is doing its job. From both, if compare the instance at epochs 75 in the left plot the validation accuracy is nearly 20% less than training accuracy whereas in the right side plot the same difference is about 5-6%, and nearly the same is maintained throughout the training at an early stage only model tried to overcome the gap.
Through this post, we have seen what needs regularization and what is regularization in deep learning in deep learning. Practically we have seen how Keras regularizer can be used in modeling to overcome the overfitting problem.