Optimising hyperparameters is considered to be the trickiest part of building machine learning and artificial intelligence models. It is nearly impossible to predict the optimal parameters while building a model, at least in the first few attempts. That is why, we always go by playing with the hyperparameter to optimise them. However, this is not scalable for high dimensional data because the number of the increase in iterations, which in turn expands the training time.

When it comes to tuning hyperparameters while developing a neural network, mastering the optimisation technique is a big pain. As this is a big part of deep learning, if these parameters are not set to optimal, the training might take ages to complete, or the model may never even reach the local minima. There are various training methods introduced into machine learning to find these optimal parameters, so let us look at two of the widely used and easy to implement techniques.

Hyperparameter Tuning Methods

Hyperparameter tuning refers to the shaping of the model architecture from the available space. This, in simple words, is nothing but searching for the right hyperparameter to find high precision and accuracy. There are several parameter tuning techniques, but in this article, we shall look into two of the most widely-used parameter optimiser techniques

• Grid search
• Random search

Grid Search

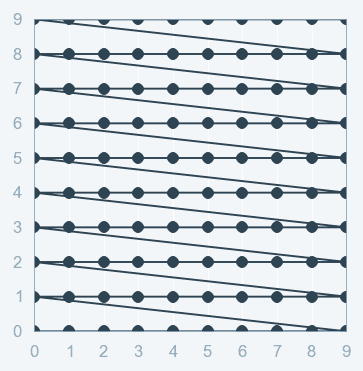
Grid search is a technique which tends to find the right set of hyperparameters for the particular model. Hyperparameters are not the model parameters and it is not possible to find the best set from the training data. Model parameters are learned during training when we optimise a loss function using something like a gradient descent. In this tuning technique, we simply build a model for every combination of various hyperparameters and evaluate each model. The model which gives the highest accuracy wins. The pattern followed here is similar to the grid, where all the values are placed in the form of a matrix. Each set of parameters is taken into consideration and the accuracy is noted. Once all the combinations are evaluated, the model with the set of parameters which give the top accuracy is considered to be the best. Below is a visual description of uniform search pattern of the grid search.

Performing grid search over the hyperparameter space with support vector machine

With the above parameters, the SVM would yield

One of the drawbacks of grid search is that when it comes to dimensionality, it suffers when evaluating the number of hyperparameters grows exponentially. However, there is no guarantee that the search will produce the perfect solution, as it usually finds one by aliasing around the right set.

Random Search

Random search is a technique where random combinations of the hyperparameters are used to find the best solution for the built model. It is similar to grid search, and yet it has proven to yield better results comparatively. The drawback of random search is that it yields high variance during computing. Since the selection of parameters is completely random; and since no intelligence is used to sample these combinations, luck plays its part.

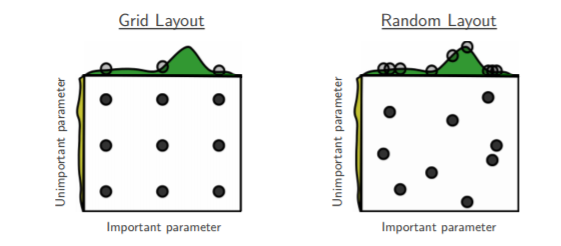
Below is a visual description of search pattern of the random search:

As random values are selected at each instance, it is highly likely that the whole of action space has been reached because of the randomness, which takes a huge amount of time to cover every aspect of the combination during grid search. This works best under the assumption that not all hyperparameters are equally important. In this search pattern, random combinations of parameters are considered in every iteration. The chances of finding the optimal parameter are comparatively higher in random search because of the random search pattern where the model might end up being trained on the optimised parameters without any aliasing.

Let us say we have 3×3 set of parameters. There are about 9 set parameters in each search technique. From the example above, random search works best for lower dimensional data since the time taken to find the right set is less with less number of iterations. In grid search, however, the optimal parameter is not found since we do not have it in our grid, and that’s why time is spent to find the near best solution is until it reaches the last set sample. With this example, it is clear that random search is the best parameter search technique when there are less number of dimensions.

While providing the information for the search parameters, for example, the properties of the cost function like continuous or discrete and type or property of error correction like stochastic, all these parameters and the heuristics provided will help the model to converge at the minima faster. The bottom rule of finding the highest accuracy is that more the information you provide faster it finds the optimised parameters.

Conclusion

There are other optimisation techniques which might yield better results compared to these two, depending on the model and the data. When it comes to science, there is no luck but when it comes to randomness we hope to find the best sample with the least possible time.