Deep Learning, AI and Advanced Analytics are transforming the way we live and work on this planet. Some experts are comparing it to transformations like electricity or internet which were paradigm shifts for many industries.
Deep Learning, AI and Advanced Analytics are transforming the way we live and work on this planet. Some experts are comparing it to transformations like electricity or internet which were paradigm shifts for many industries.
Deep learning has applications like face detection/recognition, object detection/recognition, text classification, neural style transfer, text generation, OCR, comparison of fresh/stale and healthy/unhealthy food, detection of threats etc. across industries. A lot of advancements in deep learning implementation has been since Google open sourced their powerful framework Tensorflow for building deep neural networks.
In this article, we will understand the basics of Tensorflow, its advantages and value-add and also do a hands-on example to implement basic classifiers. For this, we have assumed that you have Tensorflow installed on your machine. If not, install it here.
What are Tensors?
Tensors are objects similar to arrays and matrices but are more powerful. Tensors can be thought of as generalised matrices which support dynamic calculations in a systemic environment of similar objects. They are important building blocks of what is called a computational graph. Tensors are useful for deep learning as it involves a lot of neural networks and neural network calculations (forward and backward propagation) can be better represented as computational graph.
The number of dimensions in a tensor is called its rank.
| N-dimensions | Type | Example | Tensor Rank |
| N=0 | Scalar | 431, 290.78, 150+4j | 0 |
| N=1 | Vectors | [2, 3, 5, 7, 11] | 1 |
| N=2 | Matrices | [ [4, 9], [16, 25] ] | 2 |
| N=3 | Matrices | [ [1, 3,7], [2, 5,8] ] | 3 |
| N>2 | Matrices | Any n-dimensional arrays | N |
What is a computational graph?
Computational graphs are a method to perform hierarchical calculations in a systematic way. Suppose there are two matrices or tensors W and X with dimensions (p1 x p2) and (n x p1). The following calculation needs to be performed on these:
- Multiply X and W and call it Z
- Apply a sigmoid function (1/1+exp(-Z)) on the multiplication
This is the kind of computation which goes inside hidden (more appropriately output layer because it is sigmoid function) layers of a neural network shown below
Fig1: A representative neural network
Here, p1 is 5 and p2 is 7. N is the number of input records. The output Z would have a dimension of (n x p2).
The above computation is a hierarchical calculation and can be represented as a computational graph as shown below.
 Fig2: A representative computational graph
Fig2: A representative computational graph
In a deep neural network, such calculations need to be performed several times – first across layers giving rise to different X and W matrices (or tensors) and second across several iterations wherein the same calculations need to be performed again with updated values of Ws. This dynamic nature of the parameters like W is facilitated well by the tensors and that is a big differentiator for them compared to matrices.
The value of a tensor depends upon the changes in the other tensors present in their ecosystem or the connected computational graph. Any tensor can be represented as a matrix but not all matrices have the inherent dynamic properties of the tensors.
Why Tensors for Deep Learning?
Neural networks, especially deep neural networks, are complex Computational Flow Graphs with many layers of connected neurons and weights (parameters) and require a lot of computational effort on multidimensional arrays.
Reasons, why tensors are suitable for deep neural networks, are as follows:
- Tensors provide easy method to create dynamic parameters
- These parameters, being tensors, can also handle large data sizes
- Defining and maintaining parameters is easy hence a large number of parameters can be handled
What does the name Tensorflow mean?
Tensorflow is a combination of two words:
Tensorflow = Tensor + Flow
Tensors = Dynamic multi-dimensional arrays/matrices
Flow = Computations as Computational Flow graphs
Every computable operation can be represented as a Computation Flow Graph . Computation Flow Graphs, as illustrated above, are the computational architectures where the nodes represent the Operations (like addition, division, or multiplication) and the edges represent the multidimensional arrays (Tensors) flowing to those operations.
Value Add from Tensorflow
Tensorflow makes the life of a Deep Learning programmer and a researcher much easier.
A deep neural network requires several types of computations/tasks which needs to be done several times. Some of these tasks are as follows:
Computation – Matrix Multiplication, Batch Normalisation
Activation Functions – Sigmoid, Tanh, Softmax, ReLu, Leaky ReLu
Regularisation – Dropout
Loss function Optimisers – Gradient Descent, Adam, RMSprop
Special operations – Convolution, Max/Avg Pooling, Full Connection
Each of these are specialised tasks and need their own parameters. The main value add of Tensor Flow or any other similar framework (Keras, Pytorch etc.) is that they give readymade APIs/functions to implement these tasks in one liners. Hence, the architect and engineer can invest the maximum amount of time in deciding the best architecture of the neural network and spend minimal time on coding the building blocks of the network and training the network.
1) The availability of these APIs saves a lot of time. Even a novice programmer with a good understanding of the architecture and maths can implement a deep neural network using TensorFlow framework.
2) Prototyping of new architectures is very agile using this framework. For this reasons, researchers can use it to prototype and select the best architecture for the deep network.
3)Tensorflow’s inbuilt visualization library Tensorboard provides the essential space for the visualising the training parameters and monitor the health of training while training.
4)Very active open source community and robust documentation by its makers, Google.
How Tensorflow does the computations
Any calculation in Tensorflow occurs in two steps:
1)Creating a computational dataflow graph
2)Executing the computations of the graph inside a tensorflow session
Creation of the dataflow graphs is done using the basic Data Structures (Tensors Data Structures) and the basic operations (Matrix Multiplication, Sigmoid, Convolution etc.). In order to understand about the Data structures, let’s explore them a bit.
Basic Data Structures in Tensorflow
There are 3 most common Data structures in Tensorflow viz.
1)Variables
2)Constants
3)Placeholders
Constant:
Constants are the numerical constants which once declared will remain same in value.
The syntax for defining a variable is as follows:
x = tf.constant(-2.0, name=”x”, dtype=tf.float32)
Variables
Variables are the buffered elements which will store the Tensor for a specific duration of time during the graph computations.
The syntax for defining a variable is as follows:
y = tf.Variable(tf.add(tf.multiply(a, x), b))
This is used to define computations and store their results.
Placeholders:
Placeholders are a kind of promise that the engineers give to the Computational graphs that the defined data will be fed during runtime.
The syntax for defining a variable is as follows:
x = tf.placeholder(tf.float32, shape=(1024, 1024))
Session:
Sessions are the run time environment in which the nodes compute on the Tensors
Let us see how the computations are done with some examples
 Fig3: Creation of the constants and variables and running them in the session
Fig3: Creation of the constants and variables and running them in the session
The code above produces the following output.
 Fig4: Output from running the session and doing the computation in Fig.2
Fig4: Output from running the session and doing the computation in Fig.2
Let us now see how placeholders are used in calculations.
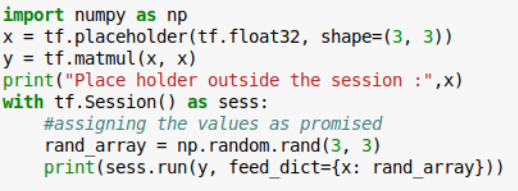 Fig 5: Calculations using placeholders in Tensorflow
Fig 5: Calculations using placeholders in Tensorflow
Notice how the feed-dict (a keyword) has been used to pass the value to the placeholder during the session run.
This code outputs the following result.
 Fig 6: Output on running the code in Fig 5
Fig 6: Output on running the code in Fig 5
What are Tensorflow estimators
The tensorflow estimators are pre-defined models which can be applied on data for training. Like Tensorflow APIs, they make defining the computations, activation functions, optimizers and regularizers very easy. Much easier than APIs but they don’t always give good results as a deep neural network implemented using APIs. Apart from that, they can help in the following tasks
- training
- evaluation
- prediction
- model weight exporting for reuse (transfer learning)
- building the graph
- initializing variables
- loading data
- handle exceptions
- create checkpoint files and recover from failures
- save summaries for TensorBoard
Tensorflow estimators are built on top of the tf.keras.layers
What is TensorBoard:
Tensorboard provides a convenient visual way to read the read the summary statistics of the training of the deep learning models.
To start the tensorboard use the following command after installation:
tensorboard –logdir=path/to/log-directory
Navigate to the “ localhost:6006 “ , and explore the tensorboard visualisations
Classifying hand-written digits (from MNIST data) using Tensorflow estimators
Let us implement a neural network classifier using Tensorflow. It will identify the actual digits from the pictures (present as arrays of pixels in the MNIST data) of hand-written digits. We are using Linear Classifier estimator in tensorflow for this implementation. Just follow along the code.
Step1: Importing the essential libraries
Step 2: Loading the data using the keras load_data function in tensorflow
In the above piece of the code we can see the type conversion, as the labels in the estimators accept only the int32 or int64 type. Default data is int8 so it needs to be typecasted.
Step 3: Feeding the input data to the tensorflow estimators using the estimator.input api
Step 4 : Creation of the necessary columns for model building
Step 5: Creation of the LinearClassifier model in Estimator
Step 6: Training the estimator model
Setp 7: Evaluating the performance over the test set
The evaluation output :
We get an accuracy of around 88%.
Step 8 : To predict the output element by element
MNIST classification by building a DNN in Tensorflow
In this sample, we explore the tensorflow end to end with a Fully Connected Deep Neural Network.
We are solving the task of Handwritten digits recognition, with a DNN architecture with:
1) 4 layered architecture
2) 1-Visible layer
3) Two hidden layers each of size 300 neurons and 200 neurons correspondingly
4) Output layer with 10 neurons
Thus the architecture being defined , we can do the step by step achievement of solving the Hand written digits task
Step 1: Import all the depending libraries and load the MNIST data
Step 2: Describe the nodes in each layer as per architecture
Step 3: Describing the placeholders to hold the data which is Features and Labels
Step 4: Defining the weights, biases and the activation function for each layer of our DNN
Step 5: Define cost function and evaluation metric
Step 6: Create an optimisation method in order to reduce the cost function
Step 7: Creating summary events.
Note that Adam Optimizer has been used to smoothen the gradients across batches as gradients in mini-batch iterations vary a lot especially in the beginning.
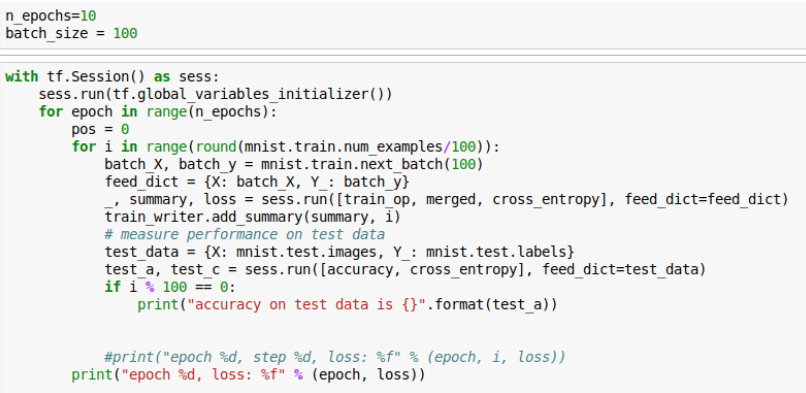
Step 8: Creating the session and running the computation for a fixed number of epochs:
Note that the number of iterations is number of total examples divided by batch size. We have implemented a mini-batch gradient descent. Here, in each epoch, all the batches (batch size=100 data points) will be used for training one after another. The model parameters will get updated after each iteration.
Output:
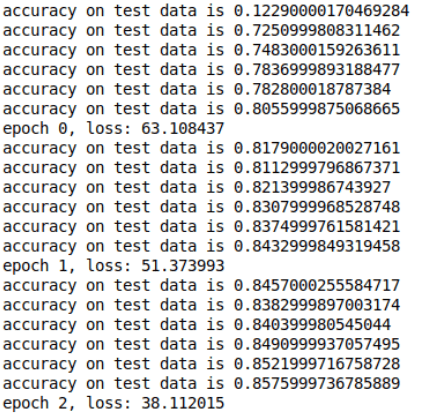
Running the session will give us the output
As you can see, as the epoch increases the loss decreases and the Accuracy on the test data increases gradually.
We can visualise the summaries using the tensorboard.