Whether it is the market crash or a wrong diagnosis, the after-effects will be certainly irreversible. Hence, tracking the development of machine learning algorithm throughout its life cycle becomes crucial. Neural network activations have an underlying compositional, combinatorial structure.
Visualising the behaviour of neural networks has been of great interest lately for two reasons — to have a glimpse at how intelligence in its fundamental form appears to be and to analyse the neurons for improvement (avoiding misclassification etc.) of the network.
Previously, AI researchers started with individual neurons. In this method, a noisy image is added with details gradually until a noticeable excitement in that neuron can be observed. But this method doesn’t show how neurons interact with each other.
The past couple of years have seen a sporadic growth of interest in interpreting the machine learning model representations and decisions made by these models, with profound implications for research into explainable ML, causality, safe AI, social science, automatic scientific discovery, human computer interaction (HCI), crowdsourcing, machine teaching, and AI ethics.
If safer AI systems are to be deployed for example, on self-driving cars, straightforward black-box models might not suffice.
Companies like Uber, use neural networks for a variety of purposes, including detecting and predicting object motion for self-driving vehicles, responding more quickly to customers, and building better maps.
The machine learning team at Uber have tried to make neural networks more transparent by introducing a new metric to assess the learning routines of a network. They call this loss change allocation(LCA). This work has also been accepted for the prestigious NeurIPS conference.
What Is Loss Change Allocation
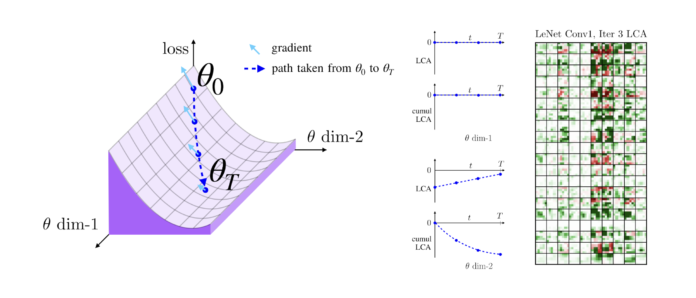
Here the objective is to measure how much each trainable parameter of the neural network “learns” at any point in time.
Think of “learning” as the changes to the network that drive training set loss down and consider the loss on the entire training set, not just a batch; while batches drive parameter updates in stochastic gradient descent. Learning is measured with respect to the whole training set.
LCA allocates changes in loss over individual parameters, thereby measuring how much each parameter learns.
This measurement is accomplished by decomposing the components of an approximate path integral along the training trajectory using a Runge-Kutta integrator.
This rich view shows which parameters are responsible for decreasing or increasing the loss during training, or which parameters “help” or “hurt” the network’s learning, respectively. LCA may be summed over training iterations and/or over neurons, channels, or layers for increasingly coarse views.
Here are few properties of LCA:
- If a parameter has zero gradient or does not move, it has zero LCA
- If a parameter has a non-zero gradient and moves in the negative gradient direction, it has a negative LCA. These parameters are called “helping” because they decrease the loss at an iteration
- If a parameter moves in the positive direction of the gradient, it is “hurting” by increasing the loss. This could be caused by a noisy mini-batch or momentum causing the parameter to move the wrong direction
Observations made using LCA:
- Barely over 50% of parameters help during any given iteration
- Some entire layers hurt overall, moving on average against the training gradient, may be due to phase lag in an oscillatory training process
- Increments in learning proceed in a synchronized manner across layers, often peaking on identical iterations
Complex machine learning models like deep neural networks have recently achieved outstanding predictive performance in a wide range of applications, including visual object recognition, speech perception, language modeling, and information retrieval.
Research has been done before on these challenges that have discerned broad patterns of convergence of layer representation, but by using LCA, layerwise learning on a smaller scale can be performed.
A useful property of the LCA method is that it allows us to analyze any loss function, which allows for a more granular view into the training process and allowing us to identify when each layer learns concepts useful for classifying.
Know more about LCA here.