We are on the cusp of a new era in computing, where the fundamental units of information processing are no longer classical bits but quantum bits, or qubits. This shift is opening up a vast, new landscape of possibilities for tackling complex mathematical problems that classical computers can’t solve efficiently. 

To give a case in point, Google quantum computers are said to be 158 million times faster than the most sophisticated supercomputer existing today—which means that the task which the Boolean logic computers will take ten years to complete, these computers will be able to do in three seconds. 

In the near future, the impact of quantum computing—spanning across a range of industries, such as finance, logistics, and cryptography—will be apparent to all.

Here is a list of some of the most popular quantum algorithms highlighting the significant impact quantum can have on the classical world: 

Shor’s Algorithm

Our entire data security systems are based on the assumption that factoring integers with a thousand or more digits is practically impossible. That was until Peter Shor in 1995 proposed that quantum mechanics allows factorisation to be performed in polynomial time, rather than exponential time achieved using classical algorithms. 

The runtime of classical factoring algorithms, such as the general number field sieve (GNFS), grows exponentially with the number of digits in the integer to be factored. Shor’s algorithm, on the other hand, is a quantum algorithm for factoring integers that has polynomial runtime, meaning that the amount of time it takes to factor an integer grows only polynomially with the number of digits in the integer.

Here is one variant of Shor’s algorithm by Alexey Kitaev, which reduces the number of qubits required to perform the factorisation, but nevertheless is able to clock a runtime roughly around d^3. 

You can check out the Qiskit implementation here. 

Grover’s Algorithm

Developed by an Indian-American computer scientist, Grover’s Algorithm is widely recognised as one of the most important quantum algorithms after Shor’s algorithm. Its primary use is to accelerate unstructured search problems quadratically, but it also serves as a valuable tool, or subroutine, to obtain quadratic run time improvements for a variety of other algorithms. 

Imagine you have a list of N items and you’re trying to find one unique item in the list. A classical computer would need to check on average N/2 items in the list to find the unique item and, in the worst-case scenario, it would have to check all N items.  However, with quantum computing, Grover’s amplitude amplification can significantly reduce the number of steps to roughly √N, which is a quadratic speedup compared to classical algorithms. 

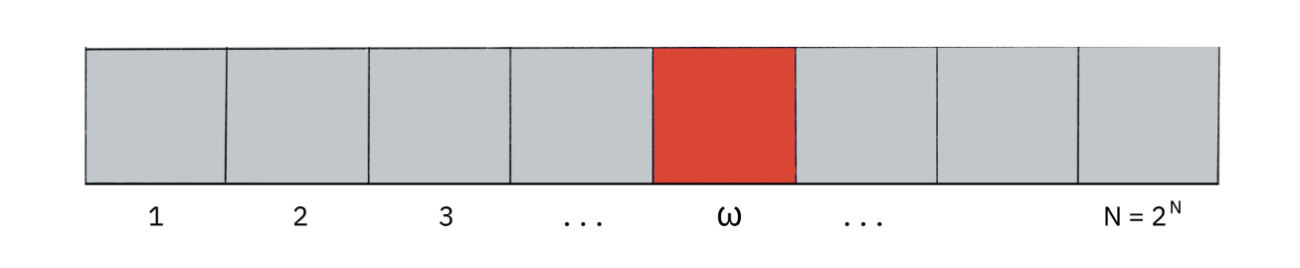
You can check out the Qiskit implementation here. 

Deutsch–Jozsa Algorithm

The Deutsch-Jozsa algorithm is a quantum algorithm designed to solve the ‘Deutsch-Jozsa problem’. This problem involves determining whether a given Boolean function is ‘constant’ (i.e., returns the same output for all possible inputs) or ‘balanced’ (i.e., returns different outputs for at least one input pair) with the least number of queries. 

For n bits as inputs, the classical algorithm requires minimum two calls to maximum 2^(n-1)+1 to be certain if a given function is constant or balanced, while the quantum computer can solve this using only one call to the function f(x).  

You can check out the Qiskit implementation here. 

Bernstein–Vazirani Algorithm

Like the Deutsch–Jozsa problem, the Bernstein–Vazirani algorithm also solves a specific black box problem. The problem involves finding s in the function f(x) = s . x, where s is some unknown string and . denotes the bitwise product (i.e., AND) operation.

Given an input x, a classical algorithm would need to call the function f(x) multiple times and use the results to determine the bits of s one at a time, requiring n calls to the function to recover the full string. However, a quantum computer can solve the problem with 100% confidence after only one call to the function f(x).

You can check out the Qiskit implementation here. 

Simon’s Algorithm

Simon’s was the first algorithm that showed an exponential speed-up versus the best classical algorithm in solving a specific problem. 

The problem at hand involves a function f(x) for there are only two outcomes—either it maps each unique input to a unique output (one-to-one) or maps two distinct inputs to one unique output (two-to-one). Additionally, there is an unknown string s which is such that for all input strings x, f(x) is equal to f(x⊕s). 

If the value of s is non-zero, then the function f is two-to-one, whereas when s is the zero string, the function f is one-to-one. Therefore, the objective is to determine whether the function f is one-to-one or two-to-one by simply finding the secret string s.

Classically, the value of s can be found for a function f with certainty by checking up to 2^(n/2) function calls. But, with quantum, using exponentially fewer queries—only a little more than n calls—a solution with 100% certainty can be found. 

You can check out the Qiskit implementation here. 

Quantum phase estimation (QPE) algorithm 

QPE is an important subroutine that serves as a central building block for many quantum algorithms. The algorithm basically estimates the phase of an eigenvalue of a unitary operator. In other words, given a unitary operator U and an eigenvector |ψ⟩ such that U|ψ⟩ = e^(2πiθ)|ψ⟩, where θ is the unknown phase angle, the goal of QPE is to estimate θ. 

It is used in a wide range of applications including quantum simulation, quantum chemistry, and optimisation. 

You can read more about it here.