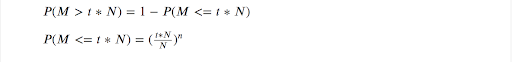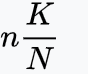A lot of us, particularly those who grew up in India, may have heard the Akbar — Birbal story, where the great Mughal emperor Akbar poses a seemingly impossible question to answer — “How many crows are there in our kingdom?”.

Birbal, the witty and intelligent minister of Emperor Akbar, retorts with a random number and when asked to prove the accuracy, responds in his typical inimitable style with the logic that Akbar cannot possibly verify since if the numbers were inaccurate, it was due to the migratory nature of birds!

However I think this is a perfectly valid estimation problem in data science and a question worth asking to a group of data scientists, if not ministers (who , if I can make an observation, never seem to understand science enough across ages!). Of course since all crows look same or indistinguishable, it seems a rather hard problem.

But before we get to crows, let us discuss a slightly adjacent problem — how do we estimate the number of cars in a city (if not kingdom). The advantage we have now of course is that unlike crows, the cars are assigned registration numbers and in most cities in more or less ascending order. An interesting point to ponder over at this point — does having such registration numbers make your task easy?

And this is a question often asked of product managers atleast in interviews — the answers hovering around a series of guesstimates around demographics, city conditions etc leading to a final “guesstimate”.

However I realized there is a elegant statistical solution to this problem, therefore making this an interesting question for a data scientist interview too. As I wrote down the mathematical proof (which we will see in a bit), a friend of mine pointed me to a mind-boggling fact that this technique was actually used almost seven decades ago in WWII by the allied forces to estimate the number of tanks that the Germans had been manufacturing, giving it the name — The German Tank problem!

The allied forces were using the captured tanks to come up with the estimate. The estimate they got was that 270 tanks being manufactured every month and later the German records post war showed the actual number to be 276! So without further ado, lets get to the approach!

Here are a few assumptions we need to make — Suppose that the registration numbers of the cars are allotted in order and without holes. Also in countries like India, there are area codes as part of the registration number — so in such cases let us focus on the problem of estimating cars within a particular area code. Also when there are letters as part of registration numbers, it should not be hard to convert them into numerical forms so that the registration number is truly a number!

Under the above assumptions / conditions, one could sample a number of cars (say n) in the city and come up with an estimate based on the maximum registration number seen.

Let us now derive what this estimate looks like — requires a bit of recollection of your high school math, in case you feel mathematically challenged. Of course, please feel free to skip to this formula directly if you like.

Suppose M is the maximum registration number seen from ’n’ samples. Suppose N is the total number cars or the actual maximum registration number allotted.

Ideally we would want M to be as close as possible to N.

That is, we want M to be greater than ∗ where 0<<=1 (And of course, we want to have t to be more closer to 1)

That is all the cars were samples from the first t * N cars in registration number order.

The above equation can be used to express the CDF function of the random variable M:

The expected value of M can be derived as follows:

In this case,

since we know that M can take values between 0 and N. Also want to clarify that this is actually a discrete random variable, though I have modelled it as a continuous random variable for calculation purposes.

For positive random variables,

Refer to link for derivation of same.

In other words, N can be estimated to be the following:

That does not look bad at all!

As an example, if you estimate M by looking at 1000 cars, M is expected to be 99.9% of the actual value!

Now that we have gotten a reasonable statistical approach to solve this problem when the cars are numbered, the question arises on what can be done in the case of the un-numbered crows! The good news is that the estimation of the population of any species is a well researched topic these days and there are techniques available to solve this seemingly hard problem.

There are two approaches to avian population estimation. One is to do a point count which is counting birds visible from a point and then extrapolate across regions. The other method is to count from a line transect and in fact if the distance information of the spotted bird is recorded, it can be used to plot a density map of the particular species of the bird in the region.

The other method is a technique called Mark and Re-capture. The biologist (or data scientist in this case!) marks a few birds of the species and lets them into the environment. After sufficient passage of time, the species is spotted and the number of marked vs unmarked birds are counted. The proportion of marked to unmarked birds in that sample enables them to extrapolate the count of the unmarked species and get an overall estimate of the population. For those inquisitive, the marking technique for birds like crows could be spraying of fluorescent dyes that could stick to the birds.

Suppose that K crows were marked. Suppose n crows were recaptured.

Out of the recaptured birds, suppose k of them were marked.

How do we determine N, the total number of crows in that locality?

Let us first understand the conditional distribution at play here.

P(k | N) = Probability of k marked birds being re-captured assuming there are N birds totally.

This turns out to be a hyper-geometric distribution. The mean of the hyper-geometric distribution is

If we have done enough observations and k turns out to be the mean of our samples, then N can be estimated to be:

Note that in both the above problems (crows and cars), I have used what is the called a frequentist approach for understanding purposes, since it is a simpler, yet reasonable approach for this problem, though there are enough cases where a frequentist approach can be prove to be a fallacy.