Last updated October 7, 2021
In AI Mysteries

A Hands-on Guide To Hybrid Ensemble Learning Models, With Python Code

In this article, we will show a heterogeneous collection of weak learners to build a hybrid ensemble learning model. Different types of machine learning algorithms are grouped together in this task to work on a classification problem. We will show the performance of individual weak learning models and then the performance of our hybrid ensemble model.

Share

Published on May 7, 2020

by Dr. Vaibhav Kumar

Ensemble learning techniques have a long record of showing better performance in a variety of machine learning applications. The domains of these applications include classification and regression problems. Random forest model and gradient boosting model are well-known ensemble models where they use a combination of weak learners to build up an ensemble. In these models, the collection of weak learners is homogeneous that means the same types of weak learners are grouped together to show their combined strength. In this article, we will show a heterogeneous collection of weak learners to build a hybrid ensemble learning model. Different types of machine learning algorithms are grouped together in this task to work on a classification problem. We will show the performance of individual weak learning models and then the performance of our hybrid ensemble model.

What is Ensemble Learning?

The ensemble learning is a concept of machine learning where the combined power of machine learning models is employed in a learning problem such as a classification problem or a regression problem. In this approach, several homogeneous machine learning models are taken as weak learners and they are grouped together. When applied to the problem, each of the weak learners shows its own result either on the entire training set or on a fraction of the entire training set. Finally, the results of each weak learner are combined together to obtain the final result.

There are two popular categories of ensemble learning, one is called as the bagging and other is called the boosting. Random forest is the popular ensemble learning model that comes under the bagging category. AdaBoost is another popular ensemble learning model that comes under the boosting category. The bagging models work on a fraction of the entire dataset while the boosting models work on the entire dataset. For more details, please refer to the article A Primer to Ensemble Learning – Bagging and Boosting.

Hybrid Ensemble Model

In this task, the five different types of machine learning models are used as weak learners to build a hybrid ensemble learning model. These models are – Logistic Regression Model, Decision Tree, Support Vector Machine, K-Nearest Neighbor Model, and the Naive Bayes Model. The term hybrid is used here because, in other ensemble models, a homogeneous collection of weak learners is used but in this task, a heterogeneous collection of weak learners is used.

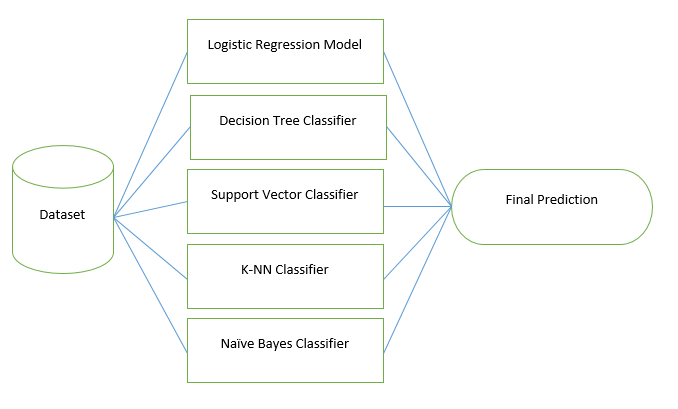
The hybrid ensemble learning model, built using these weak learning models, is applied in the task of classification for the bank’s customer churn modelling.

About the Dataset

The customer churn modelling dataset is used where the task is to predict the customer’s churn prediction for a bank. This dataset is publically available on Kaggle. This dataset comprises the bank’s customers details including the number of products the customer is availing, balance, estimated salary etc. It comprises the record of 10,000 customers with 13 attributes. The target attribute is a binary variable indicating whether the customer has exited from the bank or not.

Performance of Weak Learners

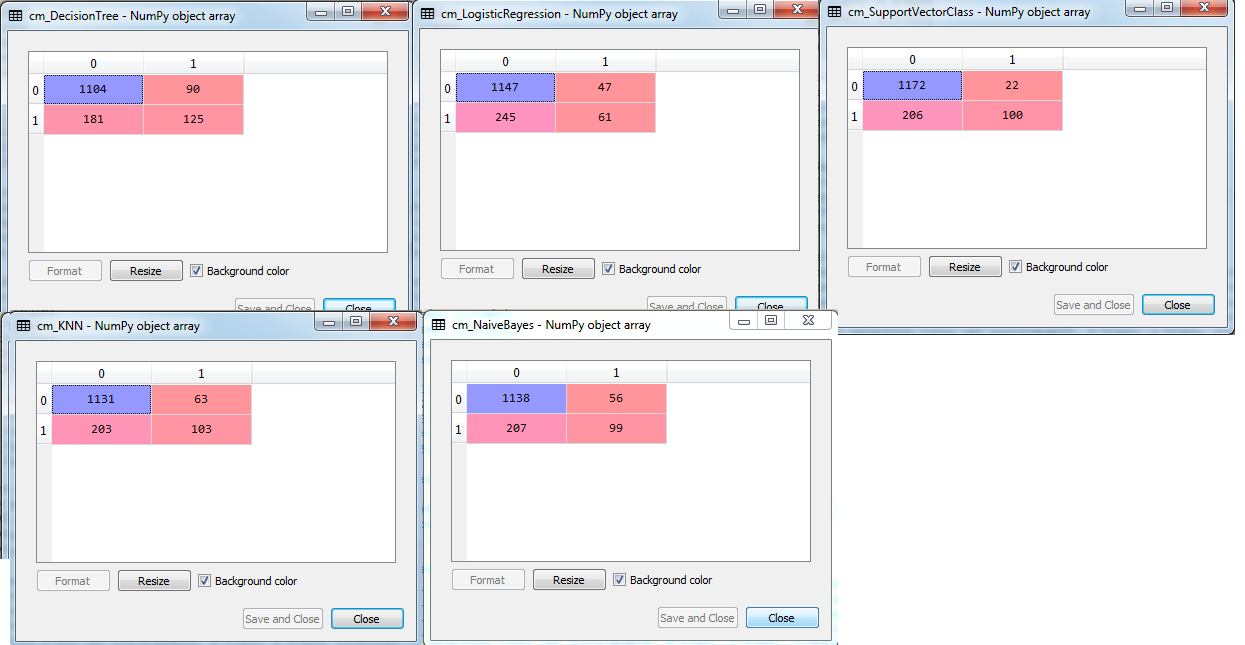
Now let us have a look at the performance of every individual machine learning model in customer churn prediction. We have trained the five machine learning models including Logistic Regression Model, Decision Tree, Support Vector Machine, K-Nearest Neighbor Model, and the Naive Bayes Model on predicting the exit of customers from the bank. The classification accuracies have been compared using the confusion matrices of each of the models. For more validation, we have performed the 10-fold cross-validations and seen the accuracies of each of the five models.

Refer to the below python implementation for the above-mentioned purpose.

#Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import VotingClassifier
from sklearn import model_selection
from sklearn.metrics import confusion_matrix
from sklearn. preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

#Reading the dataset
dataset = pd.read_csv('Churn_Modelling.csv')
X = dataset.iloc[:, 3:13].values
y = dataset.iloc[:, 13].values

# Encoding categorical data
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder()
X[:, 1] = labelencoder_X_1.fit_transform(X[:, 1])
labelencoder_X_2 = LabelEncoder()
X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2])
from sklearn.compose import ColumnTransformer
t = ColumnTransformer([("Geography", OneHotEncoder(), [1])], remainder = 'passthrough')
X = ct.fit_transform(X)
X = X[:, 1:]

# Splitting the dataset into the Training set and Test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.15, random_state = 0, stratify = y)

# Feature Scaling
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

#Defining the machine learning models
model1 = LogisticRegression()
model2 = DecisionTreeClassifier(max_depth = 2)
model3 = SVC()
model4 = KNeighborsClassifier(n_neighbors = 5, metric = 'minkowski', p = 2)
model5 = GaussianNB()

#Training the machine learning models
model1.fit(X_train, y_train)
model2.fit(X_train, y_train)
model3.fit(X_train, y_train)
model4.fit(X_train, y_train)
model5.fit(X_train, y_train)

#Making the prediction
y_pred1 = model1.predict(X_test)
y_pred2 = model2.predict(X_test)
y_pred3 = model3.predict(X_test)
y_pred4 = model4.predict(X_test)
y_pred5 = model5.predict(X_test)

#Confusion matrix
cm_LogisticRegression = confusion_matrix(y_test, y_pred1)
cm_DecisionTree = confusion_matrix(y_test, y_pred2)
cm_SupportVectorClass = confusion_matrix(y_test, y_pred3)
cm_KNN = confusion_matrix(y_test, y_pred4)
cm_NaiveBayes = confusion_matrix(y_test, y_pred5)



#10-fold cross-validation 
kfold = model_selection.KFold(n_splits=10, random_state = 0)
result1 = model_selection.cross_val_score(model1, X_train, y_train, cv=kfold)
result2 = model_selection.cross_val_score(model2, X_train, y_train, cv=kfold)
result3 = model_selection.cross_val_score(model3, X_train, y_train, cv=kfold)
result4 = model_selection.cross_val_score(model4, X_train, y_train, cv=kfold)
result5 = model_selection.cross_val_score(model5, X_train, y_train, cv=kfold)

#Printing the accuracies achieved in cross-validation
print('Accuracy of Logistic Regression Model = ',result1.mean())
print('Accuracy of Decision Tree Model = ',result2.mean())
print('Accuracy of Support Vector Machine = ',result3.mean())
print('Accuracy of k-NN Model = ',result4.mean())
print('Accuracy of Naive Bayes Model = ',result5.mean())
#Output:-

Hybrid Ensemble Learning Model

In this work, we have defined each of the five machine learning models 5 times that results in a combination of a total of 25 weak learners. Then finally, then Max Voting Classifier method is used where the class which has been predicted mostly by the weak learners will be the final class prediction of the ensemble model.

#Defining Hybrid Ensemble Learning Model
# create the sub-models
estimators = []

#Defining 5 Logistic Regression Models
model11 = LogisticRegression(penalty = 'l2', random_state = 0)
estimators.append(('logistic1', model11))
model12 = LogisticRegression(penalty = 'l2', random_state = 0)
estimators.append(('logistic2', model12))
model13 = LogisticRegression(penalty = 'l2', random_state = 0)
estimators.append(('logistic3', model13))
model14 = LogisticRegression(penalty = 'l2', random_state = 0)
estimators.append(('logistic4', model14))
model15 = LogisticRegression(penalty = 'l2', random_state = 0)
estimators.append(('logistic5', model15))

#Defining 5 Decision Tree Classifiers
model16 = DecisionTreeClassifier(max_depth = 3)
estimators.append(('cart1', model16))
model17 = DecisionTreeClassifier(max_depth = 4)
estimators.append(('cart2', model17))
model18 = DecisionTreeClassifier(max_depth = 5)
estimators.append(('cart3', model18))
model19 = DecisionTreeClassifier(max_depth = 2)
estimators.append(('cart4', model19))
model20 = DecisionTreeClassifier(max_depth = 3)
estimators.append(('cart5', model20))

#Defining 5 Support Vector Classifiers
model21 = SVC(kernel = 'linear')
estimators.append(('svm1', model21))
model22 = SVC(kernel = 'poly')
estimators.append(('svm2', model22))
model23 = SVC(kernel = 'rbf')
estimators.append(('svm3', model23))
model24 = SVC(kernel = 'rbf')
estimators.append(('svm4', model24))
model25 = SVC(kernel = 'linear')
estimators.append(('svm5', model25))

#Defining 5 K-NN classifiers
model26 = KNeighborsClassifier(n_neighbors = 5, metric = 'minkowski', p = 2)
estimators.append(('knn1', model26))
model27 = KNeighborsClassifier(n_neighbors = 5, metric = 'minkowski', p = 2)
estimators.append(('knn2', model27))
model28 = KNeighborsClassifier(n_neighbors = 6, metric = 'minkowski', p = 2)
estimators.append(('knn3', model28))
model29 = KNeighborsClassifier(n_neighbors = 4, metric = 'minkowski', p = 1)
estimators.append(('knn4', model29))
model30 = KNeighborsClassifier(n_neighbors = 5, metric = 'minkowski', p = 1)
estimators.append(('knn5', model30))

#Defining 5 Naive Bayes classifiers
model31 = GaussianNB()
estimators.append(('nbs1', model31))
model32 = GaussianNB()
estimators.append(('nbs2', model32))
model33 = GaussianNB()
estimators.append(('nbs3', model33))
model34 = GaussianNB()
estimators.append(('nbs4', model34))
model35 = GaussianNB()
estimators.append(('nbs5', model35))

# Defining the ensemble model
ensemble = VotingClassifier(estimators)
ensemble.fit(X_train, y_train)
y_pred = ensemble.predict(X_test)

#Confisuin matrix
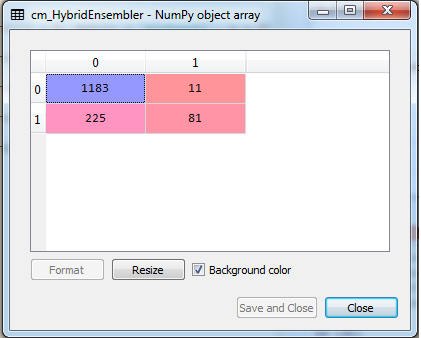
cm_HybridEnsembler = confusion_matrix(y_test, y_pred)





















#Cross-Validation
seed = 7
kfold = model_selection.KFold(n_splits=10, random_state=seed)
results = model_selection.cross_val_score(ensemble, X_train, y_train, cv=kfold)
print(results.mean())
#Output:-

As we can see the comparisons here, the hybrid ensemble learning model has outperformed all the individual learning model. We can verify this by observing the confusion matrices and cross-validation score of each individual model and the ensemble model. In future, we can make more hybrid ensemble models by adding more varieties of weak learners. We can also have a group of similar models with varying architectures.

Access all our open Survey & Awards Nomination forms in one place

Dr. Vaibhav Kumar

Dr. Vaibhav Kumar is a seasoned data science professional with great exposure to machine learning and deep learning. He has good exposure to research, where he has published several research papers in reputed international journals and presented papers at reputed international conferences. He has worked across industry and academia and has led many research and development projects in AI and machine learning. Along with his current role, he has also been associated with many reputed research labs and universities where he contributes as visiting researcher and professor.