Probabilistic Neural Networks (PNNs) are a scalable alternative to classic back-propagation neural networks in classification and pattern recognition applications. They do not require the large forward and backward calculations that are required by standard neural networks. They can also work with different types of training data. These networks employ the concept of probability theory to minimize the mis-classifications when applied to a classification problem. In this article, we will discuss Probabilistic Neural Networks in detail along with their working, advantages, disadvantages and applications. The major points to be discussed in this article are outlined below.

Table of Contents 

1. What is Probabilistic Neural Network (PNN)
2. Preliminary Concepts
3. Structure of PNN
4. Algorithm of PNN
5. Advantages and Disadvantages of PNN
6. Applications of PNN

Now let us begin with understanding the probabilistic neural networks in detail.

What is Probabilistic Neural Network?

A probabilistic neural network (PNN) is a sort of feedforward neural network used to handle classification and pattern recognition problems. In the PNN technique, the parent probability distribution function (PDF) of each class is approximated using a Parzen window and a non-parametric function. The PDF of each class is then used to estimate the class probability of fresh input data, and Bayes’ rule is used to allocate the class with the highest posterior probability to new input data. With this method, the possibility of misclassification is lowered. This type of ANN was created using a Bayesian network and a statistical approach known as Kernel Fisher discriminant analysis.

PNNs have shown a lot of promise in solving difficult scientific and engineering challenges. The following are the major types of difficulties that researchers have attempted to address with PNN:

• Labeled stationary data pattern classification
• Data pattern classification in which the data has a time-varying probabilistic density function
• Applications for signal processing that work with waveforms as data patterns
• Unsupervised algorithms for unlabeled data sets, etc.

Preliminary Concepts

Class-related PDFs must be estimated for classification tasks because they determine the structure of the classifier. As a result, each PDF is distinguished by a distinct set of parameters. The covariance and mean value are required for Gaussian distributions, and they are estimated from the sample data.

Assume we also have a set of training samples that are representative of the type of features and underlying classes, each labeled with the correct class. This results in learning difficulties. When we know the shape of the densities, we are confronted with a parameter estimation problem. 

Because there is no information available about class-related PDFs in nonparametric estimation, they must be estimated directly from the data set. There are numerous nonparametric pattern recognition approaches. The following nonparametric estimating approaches are conceptually linked to PNN.

Parzen Window

The Parzen-window method (also known as the Parzen-Rosenblatt window method) is a popular non-parametric method for estimating a probability density function p(x) for a specific point p(x) from a sample p(x_n) that does not require any prior knowledge or assumptions about the underlying distribution.

Let’s look at a simple one-dimensional scenario for a better understanding. The objective is to calculate the PDF p(x) at the given position x. This necessitates determining the number of samples Nh within the interval [x – h,x + h], then dividing by the total number of feature vectors M and the interval length 2h. We’ll get an estimate for the PDF at x using the specified approach.

Source

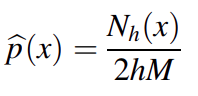
Estimating the class-conditional densities (also known as “likelihoods”) p(x|w_i)I in a supervised pattern classification issue using the training dataset where p(x) refers to a multi-dimensional sample that belongs to a particular class w_i is a prominent application of the Parzen-window technique.

K Nearest Neighbor

The length of the interval is fixed in the Parzen windows estimation, while the number of samples falling within an interval fluctuates from point to point. The opposite is true for k nearest neighbor density estimation.

The number of samples k falling within an interval is fixed, while the interval length around x is adjusted each time to include the same number of samples k. We may generalize for the n-dimensional case: The hypervolume V(x) is large in low-density areas and small in high-density areas. The estimation rule can now be given as,

Source

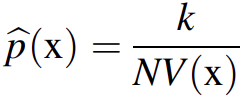
and reflects the volume V’s dependence (x). N is the total number of samples, whereas k denotes the number of points occurring within the volume V. (x).

Structure of Probabilistic Neural Network

The below is Specht’s basic framework for a probabilistic neural network (1990). The network is composed of four basic layers. Let’s understand them one by one.

Source

Input Layer

Each predictor variable is represented by a neuron in the input layer. When there are N categories in a categorical variable, N-1 neurons are used. By subtracting the median and dividing by the interquartile range, the range of data is standardized. The values are then fed to each of the neurons in the hidden layer by the input neurons.

Pattern Layer

Each case in the training data set has one neuron in this layer. It saves the values of the case’s predictor variables as well as the target value. A hidden neuron calculates the Euclidean distance between the test case and the neuron’s center point, then uses the sigma values to apply the radial basis kernel function.

Summation Layer

Each category of the target variable has one pattern neuron in PNN. Each hidden neuron stores the actual target category of each training event; the weighted value output by a hidden neuron is only supplied to the pattern neuron that corresponds to the hidden neuron’s category. The values for the class that the pattern neurons represent are added together.

Decision Layer

The output layer compares the weighted votes accumulated in the pattern layer for each target category and utilizes the largest vote to predict the target category.

Algorithm of Probabilistic Neural Network

The training set’s exemplar feature vectors are provided to us. We know the class to which each one belongs. The PNN is configured as follows.

1. Input the file containing the exemplar vectors and class numbers.
2. Sort these into K sets, each of which contains one class of vectors.
3. Create a Gaussian function centered on each exemplar vector in set k, and then define the cumulative Gaussian output function for each k.

After we’ve defined the PNN, we can feed vectors into it and classify them as follows.

1. Read the input vector and assign the Gaussian function according to their performance in each category.
2. For each cluster of hidden nodes, compute all ‘Gaussian functional useful values’ at the hidden nodes.
3. Feed all of the Gaussian functional values from the hidden node cluster to the cluster’s single output node.
4. For each category output node, add all of the inputs and multiply by a constant.
5. Determine the most valuable of all the useful values added together at the output nodes.

Advantages and Disadvantages of Probabilistic Neural Networks

There are various benefits and drawbacks and applications of employing a PNN rather than a multilayer perceptron. 

Advantages

• Multilayer perceptron networks are substantially slower than PNNs.
• PNNs have the potential to outperform multilayer perceptron networks in terms of accuracy.
• Outliers aren’t as noticeable in PNN networks.
• PNN networks predict target probability scores with high accuracy.
• PNNs are getting close to Bayes’s optimum classification.

Disadvantages

• When it comes to classifying new cases, PNNs are slower than multilayer perceptron networks.
• PNN requires extra memory to store the mod. 

Applications of Probabilistic Neural Network

Following can be the major applications of probabilistic neural networks

• Probabilistic Neural Networks can be applied to class prediction of Leukemia and Central Nervous System Embryonal Tumors.
• Probabilistic Neural Networks can be used to identify ships.
• Management of sensor setup in a wireless ad hoc network can be  done using a probabilistic neural network.
• It can be applied to Remote-sensing image classification.
• Character Recognition is also an important application of Probabilistic Neural Networks. There are many more applications of PNNs.

Final Words

We have examined different components of PNN and their multiple applications in various domains in this text. From simple pattern recognition to complicated waveform classification, these applications cover a wide range of topics. PNNs are most effective when used in conjunction with feature extraction and feature reduction approaches.

References:

• Probabilistic Neural Network
• Probabilistic neural networks: a brief overview of theory, implementation, and application