We have seen the ability of neural networks to provide best-in-class performance in a wide range of applications such as computer vision, language processing, augmented reality, etc. In spite of all of that greatness, neural networks can befall if they are not trained effectively and raise the consequences like the plateau problem. This is a phenomenon where the loss value stops decreasing during the process of learning and decelerates the performance of the optimizer algorithm. Here in this article, we will discuss the plateau phenomenon in detail with its causes and how to fix it. The following major points will be covered in this article.
Table of Contents
- Plateau Phenomenon
- Cause of the Plateau Phenomenon
- Effect of Learning Rate
- Methods to Overcome the Plateau Problem
- Scheduling the Learning Rate
- Cyclical Learning Rate
Plateau Phenomenon
However, we all have seen practically while training the neural network that after a limited number of steps, the loss function begins to slow down dramatically. After appearing to rest for a long period of time, the loss may suddenly start dropping rapidly again for no apparent cause, and this process continues till we run out of steps.
To understand it in a better way, we will refer to a few examples from a research paper by AINSWORTH and SHIN on the plateau phenomenon.
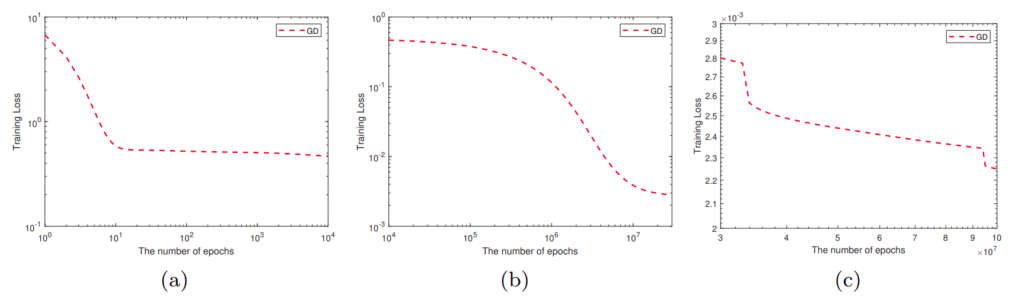
The above Training loss Vs Epoch curves are obtained for a two-layer RELU network with a width of 100 which was trying to approximate the sin(5πx) function using gradient descent optimizer with a mean squared loss and a learning rate of 0.001.
As we can see in figure 1(a), for the first 10 epochs, the loss decreases drastically but afterwards, it tends to saturate for a long period of time (literally till 10^4 epochs). After having such a long computation, the loss again tends to fall drastically as shown in figure 1(b), and then again saturates.
Many of us might conclude this model by observing the curve shown in 1(a), but the thing is that if we train our network for more epochs than the previous one then there is a chance of convergence of the model at a better point.
These Plateau events not only complicate the decision on whether to stop the gradient drop but also slow down convergence with an increasing number of seemingly superfluous iterations spent traversing a plateau before entering a new regime in which the loss decreases rapidly.
Cause of Plateau
There, in the optimization, we can see that our loss landscape may have two types of problematic areas: saddle points and local minima. Indeed, this could be the reason why our loss does not improve any further, particularly when your learning rate becomes very low at a given moment in time, either because it is programmed that way or because it has decayed to extremely low values.
Saddle Point
A loss landscape is a representation of our loss value in some space. Below is a loss landscape with a saddle point in the centre.

The loss landscapes in this case are essentially the z values for the x and y inputs of the hypothetical loss function that generated them. If they are the result of a function, we may be able to compute the derivative of that function as well. As a result, we may compute the gradient for that specific (x,y) position, as well as the direction and speed of change at that point.
By this intuition, we can say that at the saddle point of a particular function the gradient is zero and that does not represent the maximum and minimum value. The machine learning algorithm and optimization algorithm in a neural network is being optimized by the status of the gradient and if the gradient is zero the model gets stuck.
Local Minima
Indeed, when our training process encounters a local minimum, this can be a bottleneck. See the below figure shows the local minimum point in red dot;

The point, in this case, is an extremum, which is excellent, but the gradient is zero. If our learning rate is too low, you may not be able to escape the local minimum. Remember that while explaining the plateau in figure 1 (a), we noticed that the loss value in your hypothetical training situation began balancing around some constant number. This figure could reflect the local minimum.
As you can see in the above figure, on the left side there are global minima, if the learning is a little bit high then it can reach there in a few epochs. Otherwise, we need to tweak the learning rate so that it can reach global minimums.
Effect of Learning Rate
On the basis of examples in a training dataset, a neural network learns or approximates a function that optimally maps input to output. In other words, the learning rate hyperparameter determines how fast the model learns. When the weights are updated, such as at the end of a batch of training examples, it controls the amount of allocated error that is used to update the model’s weights.
This means that, given an optimal learning rate and a particular number of training iterations, a model will learn to best mimic a function with respect to available resources (for example, layers).
While an increased learning rate allows the model to learn faster, it may result in a less-than-optimal final set of weights. However, a slower learning rate may allow the model to acquire a more optimal, or perhaps a globally optimal set of weights, but it will take much longer to train.
For example, when the learning rate is excessively high, the model’s performance (such as training loss) will fluctuate over a period of training epochs. According to the theory, diverging weights are responsible for the oscillation of loss. The problem with a low learning rate is that it may never converge or it may get trapped on a suboptimal solution.
Therefore the learning rate plays an important role to overcome a plateau phenomenon, techniques like scheduling the learning rate and cyclical learning rate are used.
Methods to Overcome a Plateau Problem
The following approaches are used to overcome the plateau problem:-
Scheduling the Learning Rate
Learning rate annealing is the most widely used approach, which proposes starting with a reasonably high learning rate and gradually reducing it during training. The idea behind this method is that we want to get from the initial parameters to a range of excellent parameter values quickly, but we also want a learning rate low enough to explore the deeper, but narrower regions of the loss function.

Step decay is the most common type of learning rate annealing shown above, in which the learning rate is lowered by a certain percentage after a certain number of training epochs. More broadly, we can conclude that defining a learning rate schedule in which the learning rate is updated during training according to some predetermined rule is helpful.
Cyclical Learning Rate
Leslie Smith provided a cyclical learning rate scheduling approach with two bound values that fluctuate. A triangular update rule is the main learning rate schedule, but he also suggests using a triangular update with a fixed cyclic decay or an exponential cyclic decay.
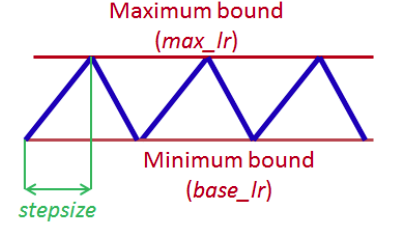
The above learning scheme shows a wonderful balance between passing over local minima while still allowing yourself to look around in detail. Rather than focusing on short-term gains, this technique focuses on long-term gains.
Conclusion
Most of us while training the network had definitely encountered this issue, especially dealing with transfer learning modules. Now going through this article, we have understood the phenomenon in detail by knowing its major cause and we can overcome this cause. There is an automated process for learning which implements the Cyclical Learning rate process. You can try it out here.