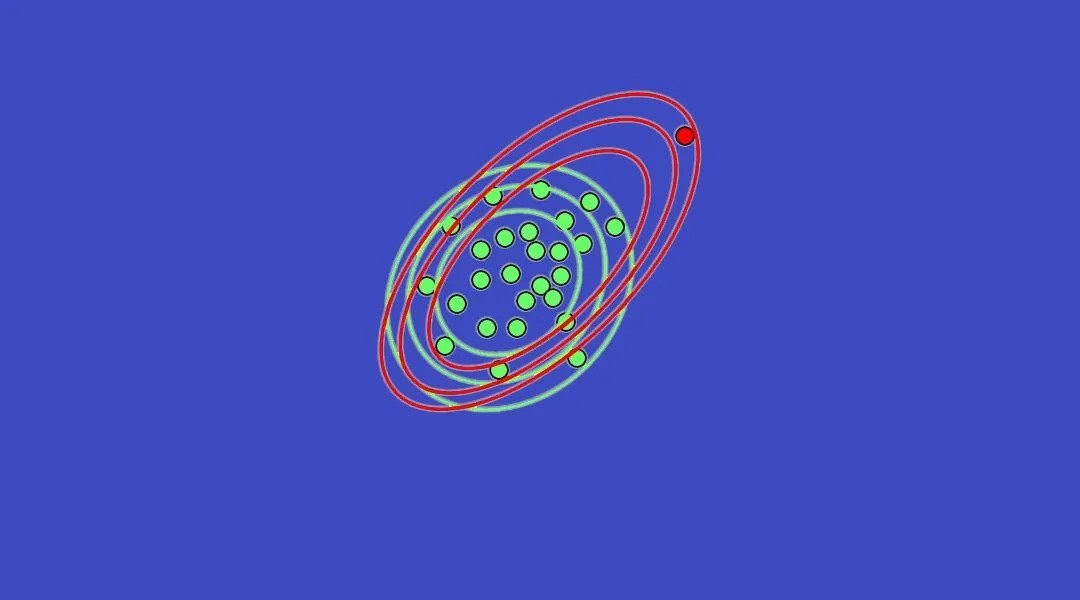
In most classification problems, the models classify the data into multiple classes. A one-class classification is an approach where the specific data elements in the dataset are separated out into a single category. Outlier detection and novelty detection are examples of one-class classification where the outlier elements are detected separately from the rest of the data elements. In this article, we will discuss the one-class classification problem and we will understand how Support Vector Machine (SVM) can be used for this purpose. The SVM used for this purpose is referred to as One-Class SVM. The major discussion points that we will cover in this article are listed below.
Table of Contents
- The One-Class Classification Problem
- Outlier Detection
- Novelty Detection
- A Basic Support Vector Machine
- SVM for One-Class Classification
Let us begin with understanding the one-class classification problems.
The One-Class Classification Problem
In many situations where we are required to detect the outlier presented in the data. Many machine learning models throw inaccuracies in the modelling of outlier elements. So it becomes a most basic requirement for us to determine if the new observation comes under the same existing distribution or if the new observation should be determined as different. These detections are often used in the process of cleaning datasets. The two most important tasks of this are discussed below.
Outlier Detection
In the training data, observations that are far from the others can be considered as outliers. Outlier estimators try to make a region fit most of the training under it ignoring the deviated observations. It can also be called unsupervised anomaly detection.
Novelty Detection
Let’s think about training data that does not consist of outliers and we want to know if the upcoming or new observation is an outlier or not. In this context, the outlier can be called a novelty. It can be considered as semi-supervised anomaly detection.
From the above intuition, we can say that if there is a situation where we have observations of only one class in the data and we want to determine whether the new observations belong to that class or not. For example, we can say a model is working with machinery where the machine needs to perform only one kind of trash on only one type of given input and the model is recording and predicting whether the attributes of the input is fine for machinery or not. Such types of problems are called one-class classification problems. In these types of problems, the task is to identify the single-class label of the specific data elements.
A Basic Support Vector Machine
Basically, the support vector machine is a machine learning model that can be used for classification and regression analysis. Mostly it is used with classification problems. Let’s consider the SVM modelling with data consisting of two classes.
One of the most important qualities of SVM is that it creates nonlinear decision boundaries by projecting the data with higher dimensions in the space using its nonlinear function. It uses its function to lift the feature space F of the observations of the I space which cannot be separated by a linear function or straight line. lifted feature space can be separated by the straight hyperplane. This hyperplane is used to separate the data of one class from the other class data. This hyperplane can be the form of a nonlinear curve.

The above image represents the hyperplanes H1, H2, H3 for separating the data points of two classes where H1 is not separating them but H2 and H3 are..fitting a hyperplane between the data points calculates the margin which can be considered as the distance of the hyperplane from the closest point which should be equal from both category data and maximum. From the above image, we can say H3 is a better fit option than the H2 where H1 is not fit at all. To avoid the overfitting of the model, slack variables are introduced which allow some data points to lie within the margin. And the constant C which is always greater than zero determines the trade-off between maximizing the margin and the number of training data points within that margin (and thus training errors).
Any hyperplane can be written as the set of points X satisfying.

Where w can be a normal vector(not necessarily normalized) to the hyperplane. The above-given example of a hyperplane shows a linear SVM . in which the decision function for a data point x can be written as
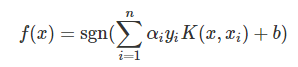
Where the function K(x, xi) is a kernel function that can be defined as
k(x,xi) = ϕ(x)Tϕ(xi)
Where ϕ is a nonlinear function. The outcome of the decision function depends on the dot vector of the vectors in the feature space. This kernel function is a very simple form of any kernel function and can be used with the data with simple distribution in space. The most commonly used kernel function is the gaussian radial basis kernel function which can be defined as:
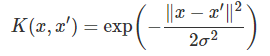
Where σ is a kernel parameter and numerator is the dissimilarity function. Using this set of functions support vector machine classifiers two classes containing data but next, we want to classify data containing only one class. Here is one class SVM that comes into the picture.
SVM for One-Class Classification
There are two different approaches from which we can learn about the One-Class SVM – one proposed by Schölkopf et al and the other proposed by Tax and Duin. Let’s talk about the first approach where the detection of novelty is done by separating the data points from the feature space and maximizing the distance from the hyperplane to the feature space. This approach results in functions that focus on the space where the density of the is maximum so that function can retire +1 if the observation is in a dense region and -1 if the observation belongs to the low dense space.
The linear SVM models minimization function can be defined as:

Where this in this approach the minimization function is

There is a slight difference of parameters in these functions in linear SVM for multiclass classification function using C parameter and this approach for one class using the parameters ν. This parameter helps in setting the upper bound on the outliers fraction and lower bound on the number of training examples that can be used for modelling with SVM.
The second approach uses a spherical boundary in the feature space where others are using the planner approach. The resulting hypersphere consists of the centre and the radius. Where the square of the radius is minimized. The centre of the hypersphere is a set of linear combinations of support vectors the minimization function for this approach is:
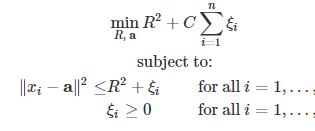
We can see that this approach is using the similarity difference of the function is the distance between the centre of the hypersphere and data points which is strictly less than the R or equal to R, which creates a dense space of the data points and the distance over than this can be considered as the outliers. To create a soft margin, slack variables are used with the parameter C.
So from the above intuition, we can say that the first approach is using the parameters to differentiate between the two-class and one-class SVM classifier and the second approach using the hypersphere to make the one class data under the sphere if the data point is the distance from the centre of the hypersphere is lower or equal to the radius.
Final words
In this article, we tried to understand one-class problems with outlier and novelty detection. We could also see various approaches to use the SVM as a one-class classifier. The main motive of the article is to explain why we use the one-class SVM for the classification of the one class. We also discussed that the hyperplane the SVM uses is the most important factor in the case of one-class classification. We discussed two approaches where the first approach uses a hyperplane but the parameters in the minimizing function are making SVM useful in One-Class SVM. The second approach uses the hypersphere for one-class classification. We can use a model from scikit-learn to implement a one-class SVM classifier.
References :