Machine Learning always works by applying changes that can make it better to learn. Not only do we need the best model for our work, but we also need to tweak the weights of the model during the training process to make our predictions as accurate as possible. Our goal is to reduce the difference or loss function.
Now you will say,
What is the loss function??
The loss function is the bread and butter of machine learning. Simply, it’s a method of evaluating how good our model is predicting. As we change pieces of our algorithm to try and improve our model, our loss function will tell us whether improvement has happened or not. You might also have heard about the cost function. Loss and cost functions are almost similar except that Loss function is calculated at every instance and the cost function is computed as an average of the loss function.
One of the most common loss functions is the Squared error loss. Squared error loss for each example of the dataset is the square of the difference between the actual and the predicted values.

Where, L is the loss function, y is the actual value and f(x) is the predicted value.
To achieve a satisfactory result we need to run our model in multiple epochs with changing the weights and biases as required. This is known as Gradient descent.
Gradient Descent:From the name we may easily get the idea, a descent in the gradient of the loss function is known gradient descent. Simply, gradient descent is the method to find a valley (comparable to minimum loss) of a mountain (comparable to loss function). To find that valley, we need to progress with a negative gradient of the function at the current point.

Where is the weight parameter of our model,
is the learning rate, and
is the gradient of cost function with respect to
Gradient descents are divided into 3 types based on the batch size which is the term used in ML and represent the number of training examples utilized in a single iteration. So, let’s discover what the three types are –
- Batch Gradient Descent or Vanilla Gradient Descent
Vanilla gradient descent aka batch gradient descent computes the gradient of the cost function i.e. it uses all the training examples in a single iteration. As we need to calculate the gradients for the whole dataset to perform just one update, batch gradient descent can be very slow and is intractable for datasets that don’t fit in memory. Because of that major problem batch gradient descent is not used in most cases.
- Stochastic Gradient Descent
In stochastic gradient descent, we use a single example to calculate the gradient and update the weights with every iteration. We first need to shuffle the dataset so that we get a completely randomized dataset. As the dataset is randomized and weights are updated for every single example, an update of the weights and the cost function will be noisy jumping all over the place. A random sample helps to arrive at a global minima and avoids getting stuck at local minima.
While batch gradient descent converges to the minimum of the mountain of loss function the parameters are placed in, SGD’s fluctuation, on the one hand, enables it to jump to new and potentially better local minima. On the other hand, this ultimately complicates convergence to the exact minimum, as SGD will keep overshooting. However, it has been shown that when we slowly decrease the learning rate, SGD shows the same convergence behaviour as batch gradient descent, almost certainly converging to a local or the global minimum for non-convex and convex optimization respectively.
- Mini batch Gradient Descent
Mini-batch gradient is a variation of gradient descent where the batch size consists more than one and less than the total dataset. Mini batch gradient descent is widely used and converges faster and is more stable. Batch size can vary depending on the dataset. As we take a batch with different samples, it reduces the noise which is the variance of the weight updates and this helps to have a more stable and faster convergence.
Just using gradient descent we can not fulfill our thirst. Here Optimizer comes in. Optimizers shape and mold our model into its most accurate possible form by updating the weights. The loss function guides the optimizer by telling it whether it is moving in the right direction to reach the bottom of the valley, the global minimum.
Let’s dive into the ocean of optimizers to know them best-
Types of Optimizers
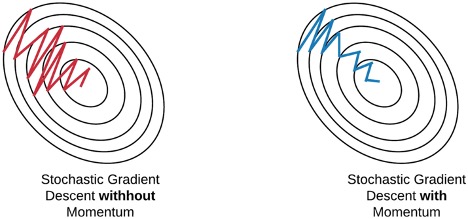
Momentum:
I guess almost all of us are familiar with the word ‘momentum’. As gradient descent is comparable with finding a valley, momentum can be compared to a ball rolling downhill. Momentum helps us to accelerate Gradient Descent(GD) when we have surfaces that curve more steeply in one direction than in another direction. It also moistens the oscillation as shown below. For updating the weights it takes the gradient of the current step as well as the gradient of the previous time steps. Momentum speeds up gradient descent by converging faster.

Where V the exponentially weighted average of past gradients, is the momentum.
Thus, we observe that the weight parameters are updated using the gradient of the previous run.
Adagrad — Adaptive Gradient Algorithm:
Adagrad is an adaptive algorithm for gradient-based optimization that alters the learning rate to a lower value for parameters associated with frequently occurring features, and larger updates (i.e. high learning rates) for parameters associated with infrequent features. For this reason, it is well-suited for dealing with sparse data.
Previously, we performed updates on the weights with the same learning rate for every weight. But Adagrad refurbishes the learning rate for every parameter .
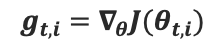
is the partial derivative of the cost function w.r.t the parameter
at the time step t.
contains the sum of the squares of the past gradients w.r.t. to all parameters θ along its diagonal. We can now vectorize our implementation by performing a matrix-vector product ⊙ between
and
:
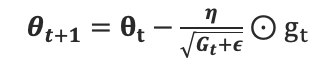
One of Adagrad’s main benefits is that it eliminates the need to manually tune the learning rate. Most implementations use a default value of 0.01 and leave it at that.
Adagrad’s main weakness is its accumulation of the squared gradients in the denominator: Since every added term is positive, the accumulated sum keeps growing during training. This in turn causes the learning rate to shrink and eventually become infinitesimally small, at which point the algorithm is no longer able to acquire additional knowledge. The following algorithms aim to resolve this flaw.
RMSProp:
RMSProp, Root Mean Square Propagation, was devised by Geoffrey Hinton inLecture 6e of his Coursera Class.. RMSProp comes up by solving the disadvantages of Adagrad. In RMSProp learning rate gets adjusted automatically and it chooses different learning rates for each parameter.

RMSprop as well divides the learning rate by an exponentially decaying average of squared gradients. Hinton suggests γ to be set to 0.9, while a good default value for the learning rate η is 0.001.
Adam:
Adaptive Moment Estimation (Adam) is another adaptive learning method. In addition to storing an exponentially decaying average of past squared gradients like Adagrad and RMSprop, Adam also keeps an exponentially decaying average of past gradients
, similar to momentum. Whereas momentum can be seen as a ball running down a slope, Adam behaves like a heavy ball with friction, which thus prefers flat minima in the error surface. We compute the decaying averages of past and past squared gradients
and
respectively as follows:
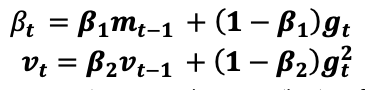
and
are the hyperparameters.
and
are estimates of the first moment (the mean) and the second moment (the uncentered variance) of the gradients respectively, hence the name of the method. As
and
are initialized as vectors of 0’s, the authors of Adam observe that they are biased towards zero, especially during the initial time steps, and especially when the decay rates are small (i.e. β1 and β2 are close to 1).
They counteract these biases by computing bias-corrected first and second moment estimates:

They then use these to update the parameters just as we have seen in Adadelta and RMSprop, which yields the Adam update rule:
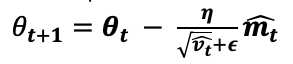
The authors propose default values of 0.9 for , 0.999 for
, and
for ϵ. They show empirically that Adam works well in practice and compares favorably to other adaptive learning-method algorithms.
Maybe I have bored you with all these theories. There are many other optimizers as well. But now I will not bore anymore. So let’s discover how good these optimizers work in some most common datasets.
Probably everyone of us have worked with MNIST dataset. There are some noticeable differences in performance of the optimizers. SGD was not good enough, as can be seen from the table below. RMSProp and Adam perform almost similarly on MNIST.

Let’s evaluate the performances of various optimizers in CIFAR10 dataset. SGD has a very steady rate of improvement and would likely benefit from more training. The issue with AdaGrad, where the learning rates increase after a few epochs, is very evident in the following table. Adam and RMSProp performed very similarly once again.
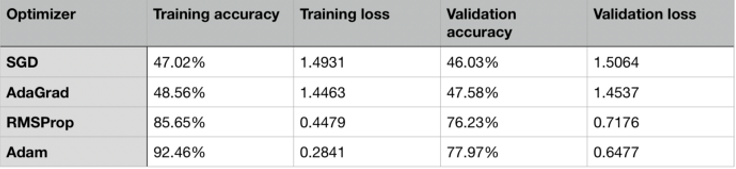
Based on these results, Adam and RMSProp are the most reliable optimizers.
Now, we have the answer to our question in the introduction image..