Activation functions are important for a Artificial Neural Network to learn and understand the complex patterns. The main function of it is to introduce non-linear properties into the network. What it does is, it calculates the ‘weighted sum’ and adds direction and decides whether to ‘fire’ a particular neuron or not. I’ll be explaining about several kinds of non-linear activation functions, like Sigmoid, Tanh, ReLU and leaky ReLU. The non linear activation function will help the model to understand  the complexity and give accurate results.

In this article, I have described some commonly used activation function. There are various activation functions and research is still going on to identify the optimum function for a specific model. Once you know the logic of the model, you can decide which activation to use.

Sigmoid Function:

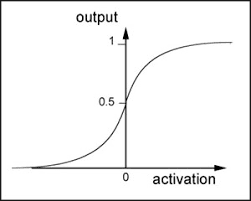
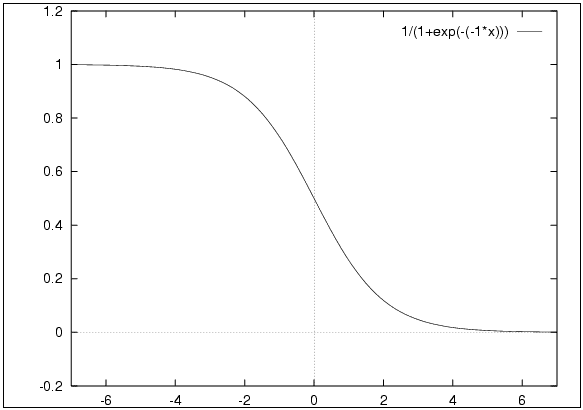
The sigmoid function is an activation function where it scales the values between 0 and 1 by applying a threshold. Below is a sigmoid curve,

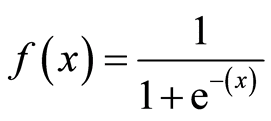The above equation represents a sigmoid function. When we apply the weighted sum in the place of X, the values are scaled in between 0 and 1. The beauty of an exponent is that the value never reaches zero nor exceed 1 in the above equation. The large negative numbers are scaled towards 0 and large positive numbers are scaled towards 1.

In the above example, as x goes to minus infinity, y goes to 0 (tends not to fire).
As x goes to infinity, y goes to 1 (tends to fire):
At x=0, y=1/2.
The threshold is set to 0.5. If the value is above 0.5 it is scaled towards 1 and if it is below 0.5 it is scaled towards 0.

We can also change the sign to implement the opposite of the threshold by the above example. With a large positive input we get a large negative output which tends to not fire and with a large negative input we get a large positive output which tends to fire.

The beauty of sigmoid function is that the derivative of the function. Once this is computed, it is easy to apply gradient descent during back propagation. It makes it smooth to gradually descent towards to minima once this is scaled while we apply the gradient descent. Here is a visual representation,

Hyperbolic Tangent:

The Tanh function is an activation function which re scales the values between -1 and 1 by applying a threshold just like a sigmoid function. The advantage i.e the values of a tanh is zero centered which helps the next neuron during propagating.
Below is a tanh function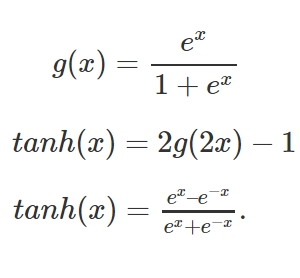When we apply the weighted sum of the inputs in the tanh(x), it re scales the values between -1 and 1. . The large negative numbers are scaled towards -1 and large positive numbers are scaled towards 1. 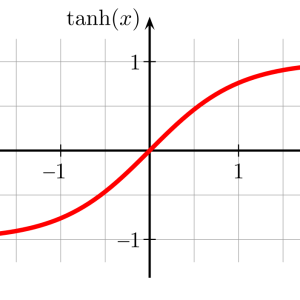In the above example, as x goes to minus infinity, tanh(x) goes to -1 (tends not to fire).
As x goes to infinity, tanh(x) goes to 1 (tends to fire):
At x=0, tanh(x)=0.
The thresold is set to 0. If the value is above 0 it is scaled towards 1 and if it is below 0 it is scaled towards -1.

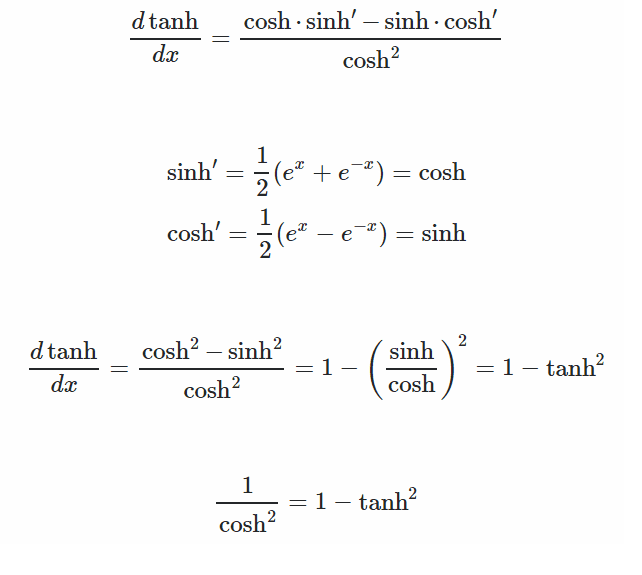This is implemented in the computation, just like the sigmoid it will smooth the curve where gradient descent will converge towards the minima based on the learning rate. Here is a visual of how it works,

ReLU(Rectified Linear Unit) :

This is one of the most widely used activation function. The benefits of ReLU is the sparsity, it allows only values which are positive and negative values are not passed which will speed up the process and it will negate or bring down possibility of occurrence of a dead neuron.

f(x) = (0,max)

This function will allow only the maximum values to pass during the front propagation as shown in the graph below. The draw backs of ReLU is when the gradient hits zero for the negative values, it does not converge towards the minima which will result in a dead neuron while back propagation.

Leaky ReLU:

This can be overcome by Leaky ReLU , which allows a small negative value during the back propagation if we have a dead ReLU problem. This will eventually activate the neuron and bring it down.

f(x)=1(x<0)(αx)+1(x>=0)(x) where α is a small constant

Some people have got results with this activation function but they are not always consistent. This activation function also has drawbacks, during the front propagation if the learning rate is set very high it will overshoot killing the neuron. This will happen when the learning rate is not set at an optimum level like in the below graph,

High learning rate leading to overshoot during gradient descent.

Low and optimal learning rate leading to a gradual descent towards the minima.

Which is the right Activation Function?

We have seen many activation functions, we need some domain knowledge to know which is the right activation function for our model. Choosing the right activation function depends on the problem that we are facing, there is no activation function which yields perfect results in all the models.

⦁ Sigmoid functions and their combinations usually work better for classification            techniques ex. Binary Classification 0s and 1s.

⦁ Tanh functions are not advised or implemented because of the dead neuron problem.

⦁ ReLU is a widely used activation function and yields beter results compared to Sigmoid and Tanh.

⦁ Leaky ReLU is a solution for a dead neuron problem during the ReLU function in the hidden layers.

There are other activation functions like softmax, selu, linear, identity, soft-plus, hard sigmoid etc which can be implemented based your model.

Image Sources: Hacknoon, Towards data science and Aharley – Ryerson University