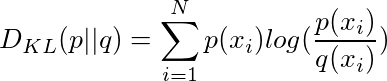All the fuel that goes into the fuel tank won’t be used completely to run the automobile. There will be dissipations (losses) and other inefficient energy transactions. That is now, a well agreed fact. Back in the 18th century, it wasn’t that obvious. So, a mathematical concept to translate the inefficiencies of a combustion engine was developed based on the experimental observations of Rudolf Clausius and later that of Carnot. It was called Entropy.
Entropy And Information Theory
Entropy is the measure of uncertainty; how disordered a system is or in this case, the degree of randomness in a set of data. Higher the entropy, lower the predictability or chances of finding patterns in the data. It can be used to explain the origin of the universe and also where the universe headed towards.
The concept of entropy or the way it is characterised had been implemented in fields remote to thermodynamics.
One such application is determining the limits of carrying out information.
The amount of information that is received as a result of an experiment/activity/event can be considered numerically equivalent to the amount of uncertainty concerning the event.
To characterise entropy and information in a much simpler way, it was initially proposed to consider these quantities as defined on the set of generalised probability distributions.
KL Divergence As A Mathematical Tool
Kullback-Leibler divergence or relative entropy is a measure of the difference between two distributions. Given by the following expression:
According to K-L divergence, whenever the probability distributions p and q are on same finite set , DKL (p || q) is the expected amount of information gained when the observer considered probability distribution as ‘q’, when in reality it is ‘p’
If the distributions under consideration are not distinct from each other then,
DKL (p || q) = 0
The lower the value of DKL (p || q), better is the approximation or the closeness of the model to
the reality.
The information gain or DKL (p || q), gives the value of information gain if q is used instead of p.
It can also be defined as the expected number of extra bits required to code samples from p using a code optimised for q.
DKL (p || q) is more relevant when it gives a Bayesian twist, according to which it is the measure of information gain when an observer/experimenter revises their assumptions from q to p.
Where ‘q’ is the prior probability distribution and ‘p’ is the posterior probability distribution.
So, here ‘q’ is the theoretical model and ‘p’ is the true model based on reality.
When the results assumptions based on ‘q’ are compared to those of ‘p’, a difference if any would be the direct indication of the amount of information gain across the process/event.
This difference, since, is a direct measure of the initial mismeasurement, it can then be approximated to ‘p’.
The Command Over Cost Function
The concept of KL divergence overlaps with both the broader f-divergences, which deals with the concept of distinction amongst distributions and, Bregman divergences which is a measure of distances, which don’t follow triangle inequality. In other words, DKL (p || q)is not equal to DKL (p || q).
One application of machine learning, where KL divergence find their direct application is the Variational AutoEncoders(VAEs). In deep learning applications, for instance, in image reconstruction or regeneration of an image similar to that of the input image.
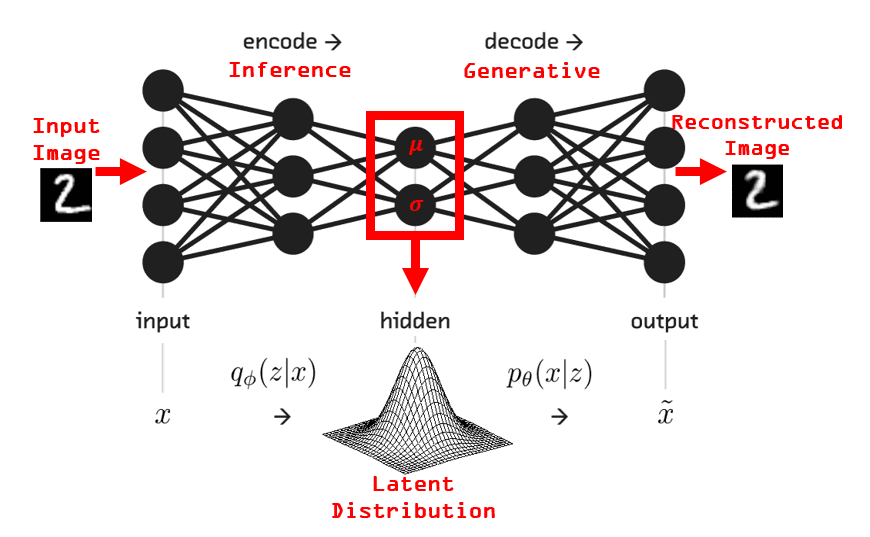
We can see above how the input image of the digit ‘2’ has been reconstructed using the autoencoder network.
Encoders can be seen in CNNs too, they convert an image into a smaller dense representation which is fed to the decoder network for reconstruction.
So, an autoencoder makes the encoder generate encodings to reconstruct its own input.
If the output image looks bit hazy than the input, it means that there has been a loss of information. This is given by the loss function of the network; cross-entropy between the output and input.
In image generation, even if the mean and standard deviation stay the same, the actual encoding will vary due to sampling.
So, in order to maintain the consistency amongst the encoders, KL divergence is introduced into the loss function. Since, KL divergence is a measure of the distinctness of the distributions, minimizing the KL divergence, would give command over the loss function, which in turn helps in keeping the output close to the reality(input).
Read more about VAEs in detail here.
Tracking Reality
KL Divergence keeps track of reality by helping the user in identifying the differences in data distributions. Since the data handles usually large in machine learning applications, KL divergence can be thought of as a diagnostic tool, which helps gain insights on which probability distribution works better and how far a model is from its target.
Read more about KL Divergence here.