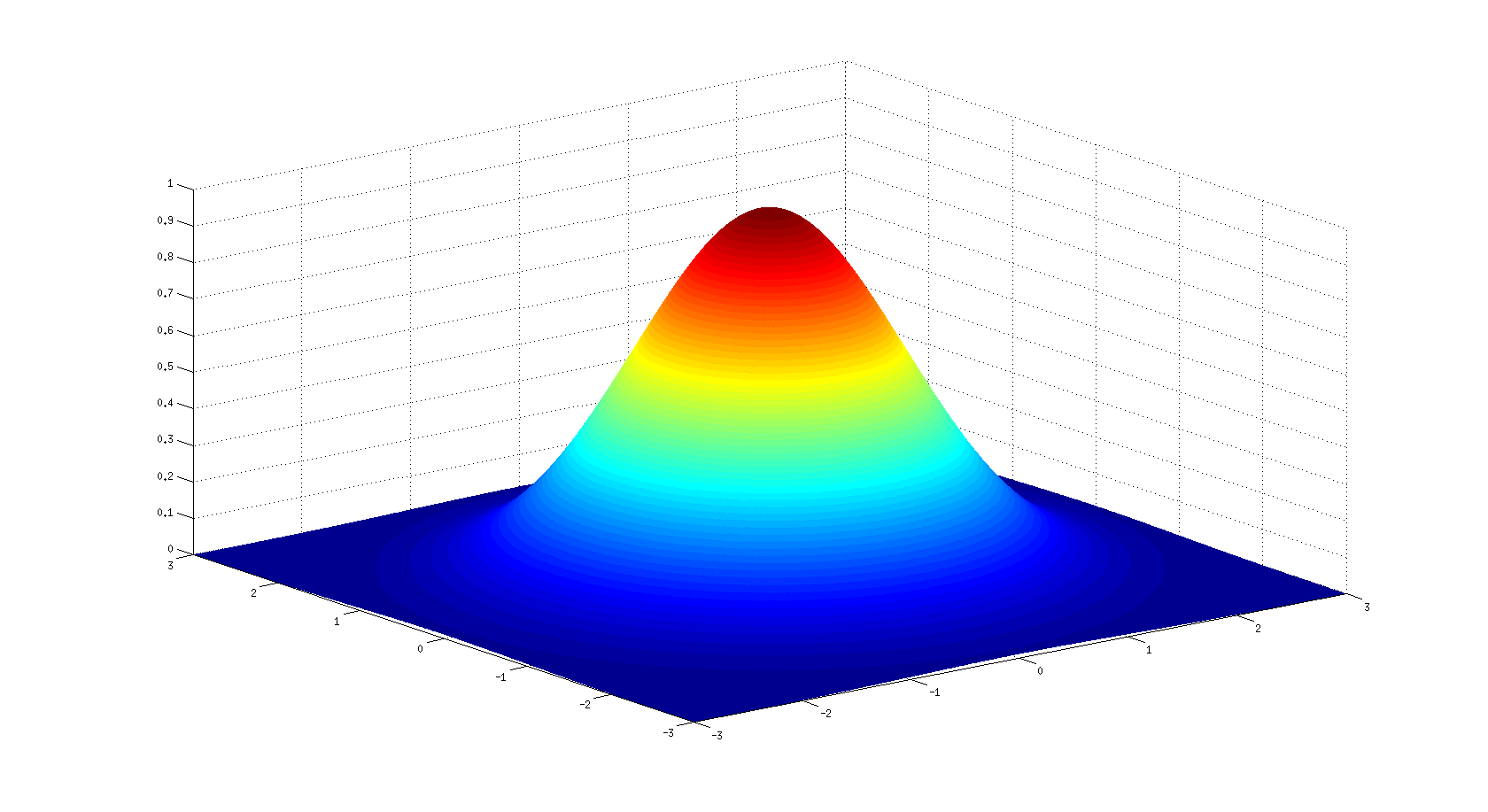
In recent times, there has been a lot of emphasis on Unsupervised learning. Studies like customer segmentation, pattern recognition has been a widespread example of this which in simple terms we can refer to as Clustering. We used to solve our problem using a basic algorithm like K-means or Hierarchical Clustering. With the introduction of Gaussian mixture modelling clustering data points have become simpler as they can handle even oblong clusters. It works in the same principle as K-means but has some of the advantages over it. It tells us about which data belongs to which cluster along with the probabilities. In other words, it performs hard classification while K-Means perform soft classification.

Here, we will implement both K-Means and Gaussian mixture model algorithms in python and compare which algorithm to choose for a particular problem.

Let’s get started.

About the dataset

The iris dataset can be downloaded from the following link. It gives the details of the length and breadth of the three flowers: Setosa, Versicolor, Virginica.

Practical Implementation

Import all the libraries required for this project.

# import some libraries
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="white", color_codes=True)
import warnings
warnings.filterwarnings("ignore")
# show plots inline
%matplotlib inline

data = pd.read_csv('Iris.csv')
data = data.drop('Id', axis=1) # get rid of the Id column - don't need it
data.sample(5)

Store the independent and dependent variable in the X,y variable.

X = data.iloc[:,0:4]
y = data.iloc[:,-1]

The data is unbalanced means some of the features are larger than others. They will dominate the dataset. To avoid this problem, we need to do feature scaling.

from sklearn import preprocessing
scaler = preprocessing.StandardScaler()
scaler.fit(X)
X_scaled_array = scaler.transform(X)
X_scaled = pd.DataFrame(X_scaled_array, columns = X.columns)
X_scaled.sample(5)

Let’s fit our model using the KMeans Algorithm. We will mention ncluster=3 as the species has 3 categories.

K-Means Clustering

from sklearn.cluster import KMeans
nclusters = 3 # this is the k in kmeans
seed = 0
km = KMeans(n_clusters=nclusters, random_state=seed)
km.fit(X_scaled)
# predict the cluster for each data point
y_cluster_kmeans = km.predict(X_scaled)
y_cluster_kmeans

import matplotlib.patches as mpatches
red_patch = mpatches.Patch(color='red', label='Setosa')
green_patch = mpatches.Patch(color='green', label='Versicolor')
blue_patch = mpatches.Patch(color='blue', label='Virginica')
colors = np.array(['blue', 'red', 'green'])
plt.scatter(X_scaled.iloc[:, 2],X_scaled.iloc[:, 3],c=colors[y_cluster_kmeans])
plt.xlabel("PetalLengthCm")
plt.ylabel("PetalWidthCm")
plt.legend(handles=[red_patch, green_patch, blue_patch])
plt.show()

The above result gives us three clusters:Setosa,Versicolor and Virginica. We can see there is some overlap between Versicolor and Virginica. So it is not easy to separate the flowers using K-Means.

from sklearn import metrics
score = metrics.silhouette_score(X_scaled, y_cluster_kmeans)
Score

The silhouette score of 0.45 shows there is the intermediate distance(neither far nor near) between the clusters.

scores = metrics.silhouette_samples(X_scaled, y_cluster_kmeans)
sns.distplot(scores);

from sklearn.metrics.cluster import adjusted_rand_score
score = adjusted_rand_score(y, y_cluster_kmeans) 
score

We can use the adjusted rand score to quantify the goodness of clustering. From the above result, KMeans gives a score of 0.62 which is pretty decent.

Gaussian Mixture Modelling Clustering

Now let’s fit the model using Gaussian mixture modelling with nclusters=3.

from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=nclusters)
gmm.fit(X_scaled)
# predict the cluster for each data point
y_cluster_gmm = gmm.predict(X_scaled)
Y_cluster_gmm

red_patch = mpatches.Patch(color='red', label='Setosa')
green_patch = mpatches.Patch(color='green', label='Versicolor')
blue_patch = mpatches.Patch(color='blue', label='Virginica')
colors = np.array(['blue', 'red', 'green'])
plt.scatter(X_scaled.iloc[:, 2],X_scaled.iloc[:, 3],c=colors[y_cluster_gmm])
plt.xlabel("PetalLengthCm")
plt.ylabel("PetalWidthCm")
plt.legend(handles=[red_patch, green_patch, blue_patch])
plt.show()

The plot displays very little overlap between the data points of different clusters. Gaussian model gives us a better result than K-Means.

from sklearn import metrics
score = metrics.silhouette_score(X_scaled, y_cluster_gmm)
Score

from sklearn.metrics.cluster import adjusted_rand_score
score = adjusted_rand_score(y, y_cluster_gmm)
score

The Gaussian mixture model has an adjusted rand score of 0.9. It gives a better fit of clustering.

Conclusion

In this article, we have discussed the basics of Gaussian mixture modelling. Further, we have compared it with K-Means with the adjusted rand score. It shows how efficient it performs compared to K-Means. Hence, it is advisable to study Gaussian mixture modelling in more depth.The complete code of the above implementation is available at the AIM’s GitHub repository. Please visit this link to find the notebook of this code.